BUILDING THE ALGORITHMS THAT SHAPE OUR WORLD

© 2025 sNoise Research Laboratory, Inc
Best viewed on Chromium-based browsers
#21st CENTURY SCIENCE

Revolutionizing Science and Industry
with Fractional Calculus
Imagine if you were sitting on a proven technology that could save the oil industry $3 billion per year—
We are actively seeking the right partners to bring it to market and transform the industry.

# FRACTIONAL CALCULUS UPGRADE
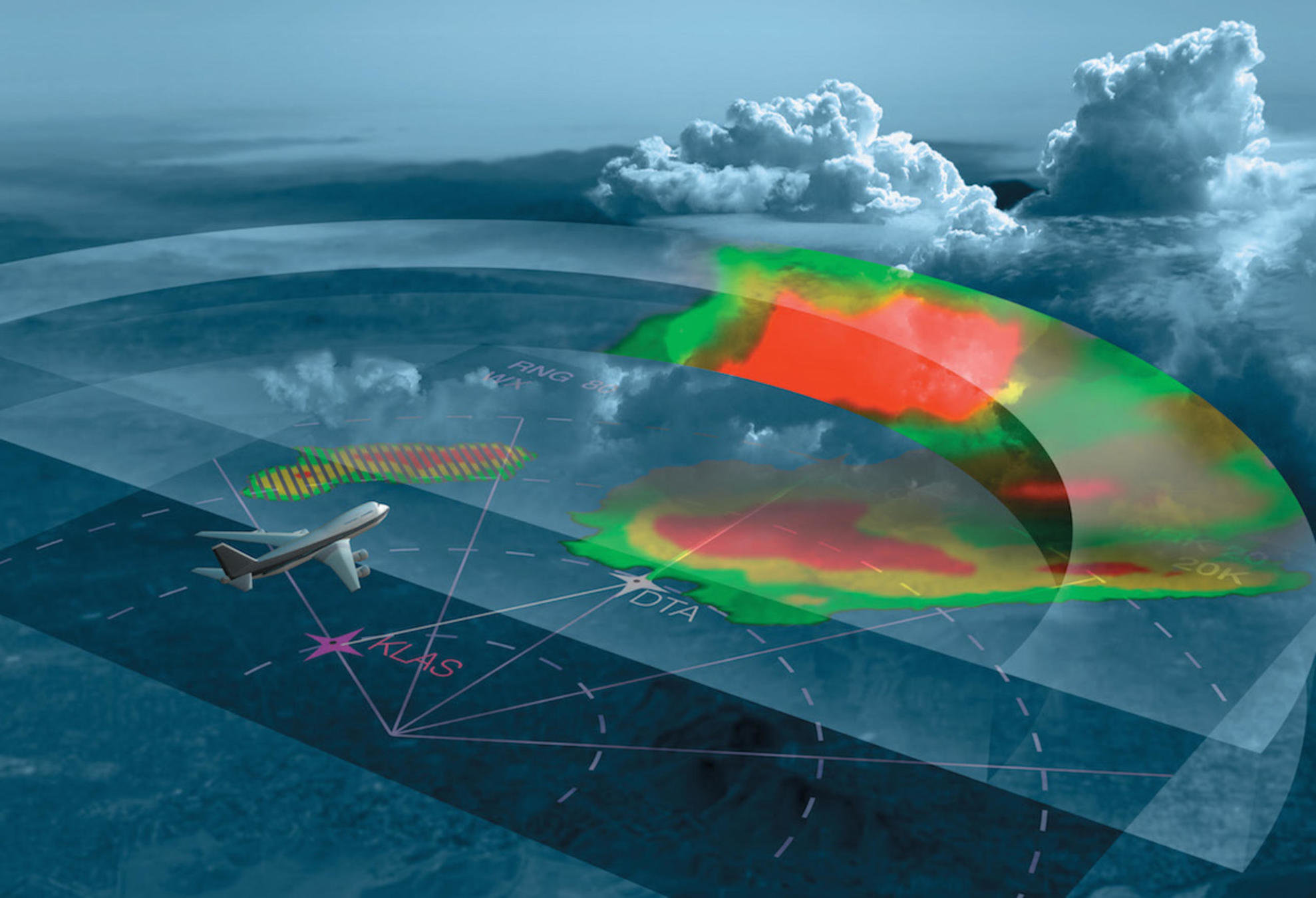
The Signal Disruption Challenge
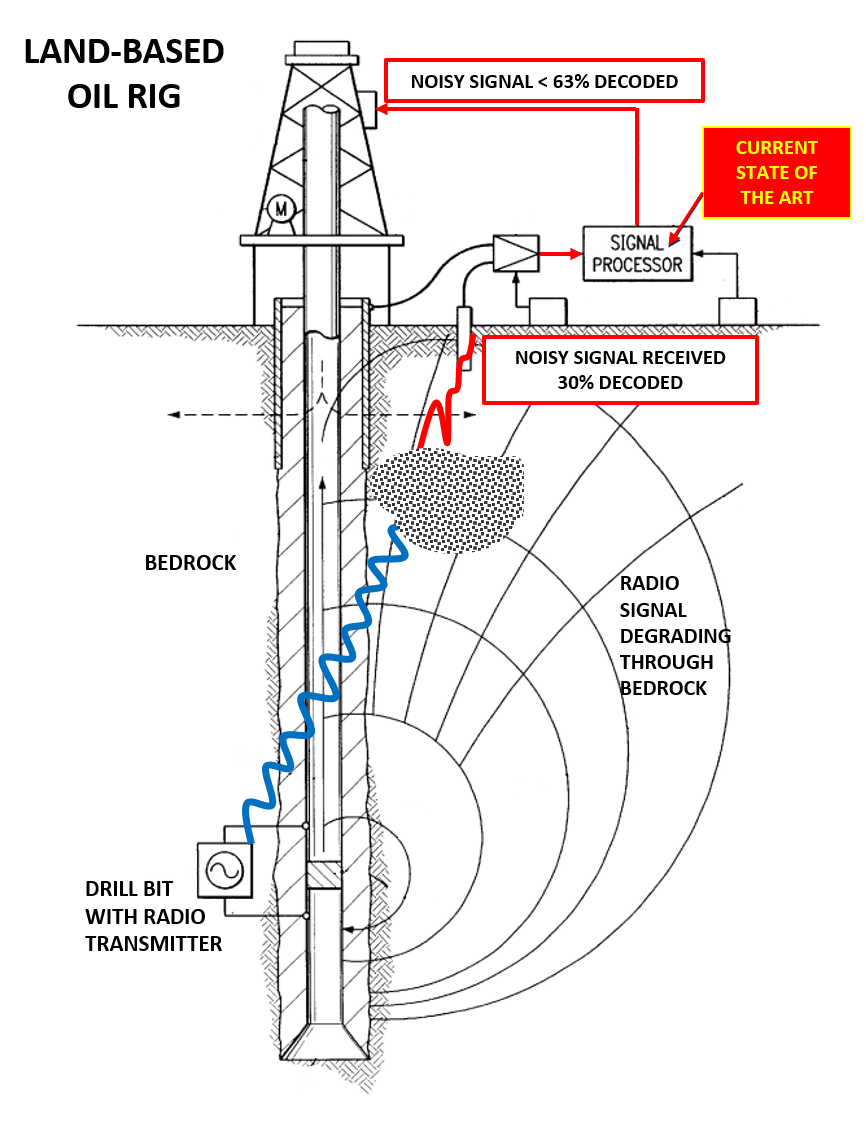


PROBLEM:
Bedrock blocks radio signals transmitted from the drill bit to land-based oil rig which introduces noise into signal preventing decoding of data.
VALUE PROPOSITION:
Restoring signal integrity and eliminating decoding errors could save the oil industry approximately $2 million per rig on average.
# FRACTIONAL CALCULUS UPGRADE
Restoring Signal Integrity:
The sNRL Solution
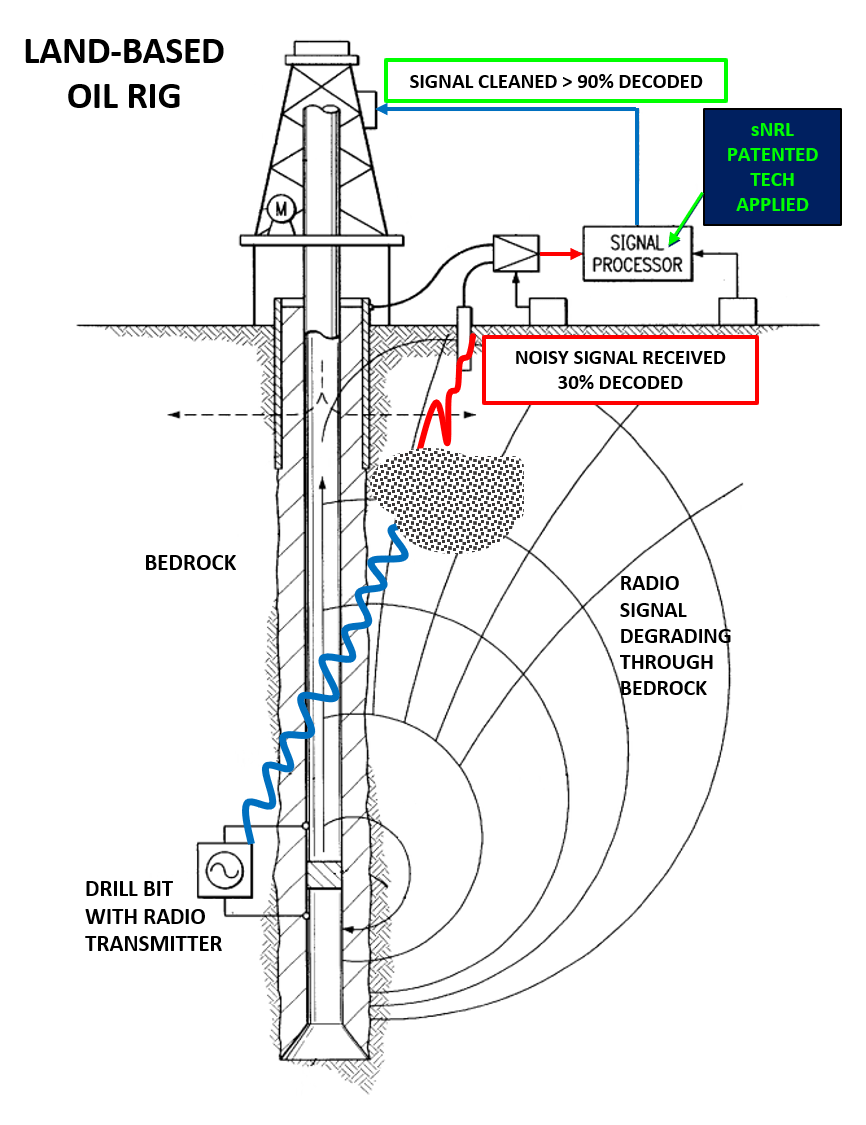


SOLUTION:
sNRL to the Rescue...
Our patented technology restores signal integrity compromised by bedrock, achieving a data decode rate greater than 90%, thereby enhancing clarity.
Fractional Calculus is an
Emerging Scientific Discipline
#21st CENTURY SCIENCE
“…the mathematical models of reality have been pushed to their limits and beyond, those which were developed and applied so successfully to the explanation and understanding of physical phenomena in the nineteenth and twentieth centuries are no longer adequate to describe the emergent phenomena of the twenty-first century. Herein we propose to adopt a fresh perspective entailed by the use of the fractional calculus.”
- Fractional Calculus View of Complexity: Tomorrow’s Science, Bruce J. West, 2016.

Defining Fractional Calculus (FC)
# FRACTIONAL CALCULUS

Fractional Calculus offers unique solutions unavailable to Calculus and is more reflective of our physical reality and how the universe works encoded within digital signals.
Fractional Calculus includes all of Traditional Calculus


We hold patents for Fractional Scaling Digital Signal Processing (FSDSP) in a computer, which employs fractional calculus equation-based algorithms for signal processing and fractional-order control systems.
◄Direct Pitch►
▼Deep Dive▲
Traditional calculus operates only with integer-order derivatives and integrals leading to oversimplified representations of real-world complex phenomena. Fractional Calculus is a superset of and extends traditional calculus to allow differentiation and integration of functions at fractional (non-integer) orders capturing complex dynamic behaviors and phenomenon.
# SIGNAL PROCESSING

Information -
The Signal in the Noise:
Signals convey information. In nature, this information may be in the form of an analog or continuous signal, such as a physical sound wave or radio wave. With proper sampling and sensors, a microphone or radio in this example, we can numerically represent this physical analog wave as a digital signal which is a discrete sequence of numbers that represents all of the information contained within that waveform.
Often when sampling the environment, our sensors collect unwanted signals, disturbances, or extra information that is not relevant to the signal and obscures the information we want to collect. This irrelevant information we term noise which interferes with our ability to extract meaningful information from the signal and can prevent technologies from working properly.
Digital Signal Processing
is a Phantom Technology:
Digital Signal Processing (DSP) is often called the Phantom Technology as DSP is in nearly all modern electronics but takes place behind the scenes as algorithms in hardware or software. More specifically, DSP is applying math encoded as algorithms in hardware or software to those numerical values of a digital signal in order to change the signal in some advantageous or useful way, such as in filtering a signal to extract the useful information as in tuning a digital radio.
As a research, development, and innovation laboratory, the sNoise Research Laboratory (sNRL) is leading the way to develop advanced Fractional Scaling Digital Signal Processing (FSDSP) tools, signal-shaping smart filters, and algorithmic mathematical solutions based on fractional calculus in order to better extract the signal from the noise to reveal the hidden reality of information shaping the technologies of our modern world.
Signal Processing
Removes Noise from the Signal:
In order to decode and clean up a signal that contains noise to make the signal useful, we filter or process the signal through electronic circuits or mathematical algorithms to separate and extract the signal from the noise. Collectively, cleaning up and filtering a signal to reduce or eliminate noise is one example of Signal Processing.
Whether we realize it or not, everyday, our lives are influenced by signals and shaped by signal processing. If you drive a car, used navigation maps with GPS, made a cell phone call, used a computer or the Internet, took a digital picture, played a video game, watched a movie on DVD, used a charge card, had a MRI or CAT scan, listened to the radio, or used RADAR or SONAR, you have used signal processing technologies.
What is Signal Processing?
# FRACTIONAL SCALING DSP (FSDSP)

Fractional Order Control Systems
for Dynamic and Emergent Robotics:
As the language of dynamic system models, FSDSP also extends to defining, modeling, and filtering of fractional order control systems (FOCS) and improves the response, stability, and machine learning capability of emergent robotic and AI platforms such as Unmanned Vehicle Systems (UAVs), self-driving vehicles, and satellites. Fractional Order Control Systems invoking FSDSP, such as a fractional order proportional-integral-derivative (PID) controller, provide greater stability and performance under strong perturbations, are more flexible and better able to adapt to dynamic properties of an environment, have more effective damping characteristics, and may recover faster and with greater accuracy from disturbances.
Applications in Multiple Markets
Industries, and Scientific Disciplines:
By utilizing a fractional calculus approach to digital signal processing, Fractional Scaling Digital Signal Processing and Fractional Scaling Digital Filters provide sNRL the ability to selectively filter complex data sets and can achieve nearly any desired filtering characteristic with a high degree of accuracy from sharp transitions within a narrow bandwidth to complicated structures within the passband, all without introducing the mathematical artifacts of current state-of-the-art filters or resulting in a loss of information in the filtered signal. FSDSP grants sNRL the ability to extract the signal from the noise more effectively with a higher resolution and level of performance than conventional digital signal processing filters and algorithms that are based on traditional integer-based calculus.
Defining Fractional Scaling Digital Signal Processing (FSDSP)
Fractional Scaling
Digital Signal Processing (FSDSP):
Fundamentally, Fractional Scaling Digital Signal Processing (FSDSP) allows fractional calculus, and thus fractional filtering (e.g., fractional scaling, fractional phase shifting, fractional integration, or fractional differentiation) to be performed on a signal. In fact, FSDSP opens up access to a signal allowing each individual frequency the ability to be adjusted to any decimal level in magnitude and/or phase and also the ability to access or alter the time element of the signal or frequency. FSDSP also encompasses a new class of digital filters (Fractional Scaling Digital Filters or FSDF) and further defines control systems (Fractional Order Control Systems or FOCS) in terms of Fractional Calculus. Representing exact filtering solutions rather than approximations, FSDSP demonstrably exhibits extreme mathematical accuracy, precision, robustness, flexibility, and computational efficiency leading to cleaner signals and more effective control.
Defining Fractional Scaling Digital Signal Processing (FSDSP)
# FSDSP AS PLATFORM TECHNOLOGY
Next-Generation
Platform Technology:
As the next generation in digital signal processing technology, Fractional Scaling Digital Signal Processing (FSDSP) represents a game-changing platform technology for the digital age, offers the potential to revolutionize the way in which we currently see, model, filter, and control digital signals and systems, and represents a remarkable technological advancement over current digital filter designs.
Multiple Dimensional
Signal Processing:
FSDSP extends to signals across multiple dimensions and may be successfully applied whether that signal is single dimensional as in 1-dimensional arrays (1D time series signals), or a 2-dimensional space (2D static imagery), 3-dimensional space and time (dynamic video or spatio-temporal dynamic texture), or 4-dimensional (2D or 3D plus a time component or spacetime) digital signal.
FSDSP acts like
Fractals for Time:
In one sense, what the discovery of fractals did for shapes and computer-generated imagery, FSDSP does for signals and time. With the Potential to become the industry standard for digital signal processing filters, sNRL's patented FSDSP algorithms may rapidly accelerate technological developments in a variety of fields to generate robust solutions for the future and reveal the true hidden nature of reality.
Simulations - FSDSP is
the mathematics of Nature:
With FSDSP, sNRL can now shape any signal, accessing every frequency in both magnitude and/or phase allowing ultra-realistic simulations, revealing hidden information about recorded and measured quantities of real-world data, electromagnetic, or physical phenomena which may also lead to detailed predictive models or filters of these complex signals and phenomena.

# FRACTIONAL CALCULUS REPOSITORY

Disruptive and Accessible
Advanced FSDSP Technology:
FSDSP provides a complete, organized mathematical framework and repository of Fractional Calculus encoded as a library of patented algorithms. sNRL is actively working towards converting the FSDSP algorithms from MATLAB to a multi-language Software Development Kit (SDK) for edge computing and Application Programming Interface (API) for cloud computing with integrated AI and deep learning algorithms. Custom interfaces and sample data for each field of use and data type are also planned for inclusion into the FSDSP SDK and API so that customers from a variety of scientific and engineering fields may more readily test, license, and implement the fractional calculus algorithms in both hardware and software products leading to widespread adoption potentially disrupting industry standards in many of these disciplines.
Applications in Multiple Markets,
Industries, and Scientific Disciplines:
The usefulness of fractional calculus and FSDSP including Fractional Scaling Digital Filters and their use in fractional order control systems extends across a multitude of disciplines and industries from control theory, cybernetics, economics, information theory, medicine, neuroscience, neuroengineering, cognitive science, and the human behavioral sciences to the environmental sciences, meteorology, geophysics, aerospace, control systems, robotics, mechanical engineering, mechatronics, sensors, electrical engineering, telecommunications, audio, video, and digital signal processing with numerous applications such as RADAR and SONAR Data Acquisition Systems. Since Fractional Calculus encompasses all of Calculus, the current possibilities and the yet undiscovered potential uses are truly limitless.
Defining Fractional Scaling Digital Signal Processing (FSDSP)
# FRACTIONAL CALCULUS
Traditional Calculus:
-
Integration is simply Addition or the cumulative summation of values of a signal.
-
Differentiation is Subtraction or the differences between adjacent values in a signal.
Limitations of Traditional Calculus:
-
Traditional calculus, demonstrated to the left, operates only with integer-order derivatives and integrals, which can struggle to accurately model complex systems with memory effects and non-linear dynamics, leading to oversimplified representations of real-world phenomena.
Example of Traditional Calculus (Single Integrator):
-
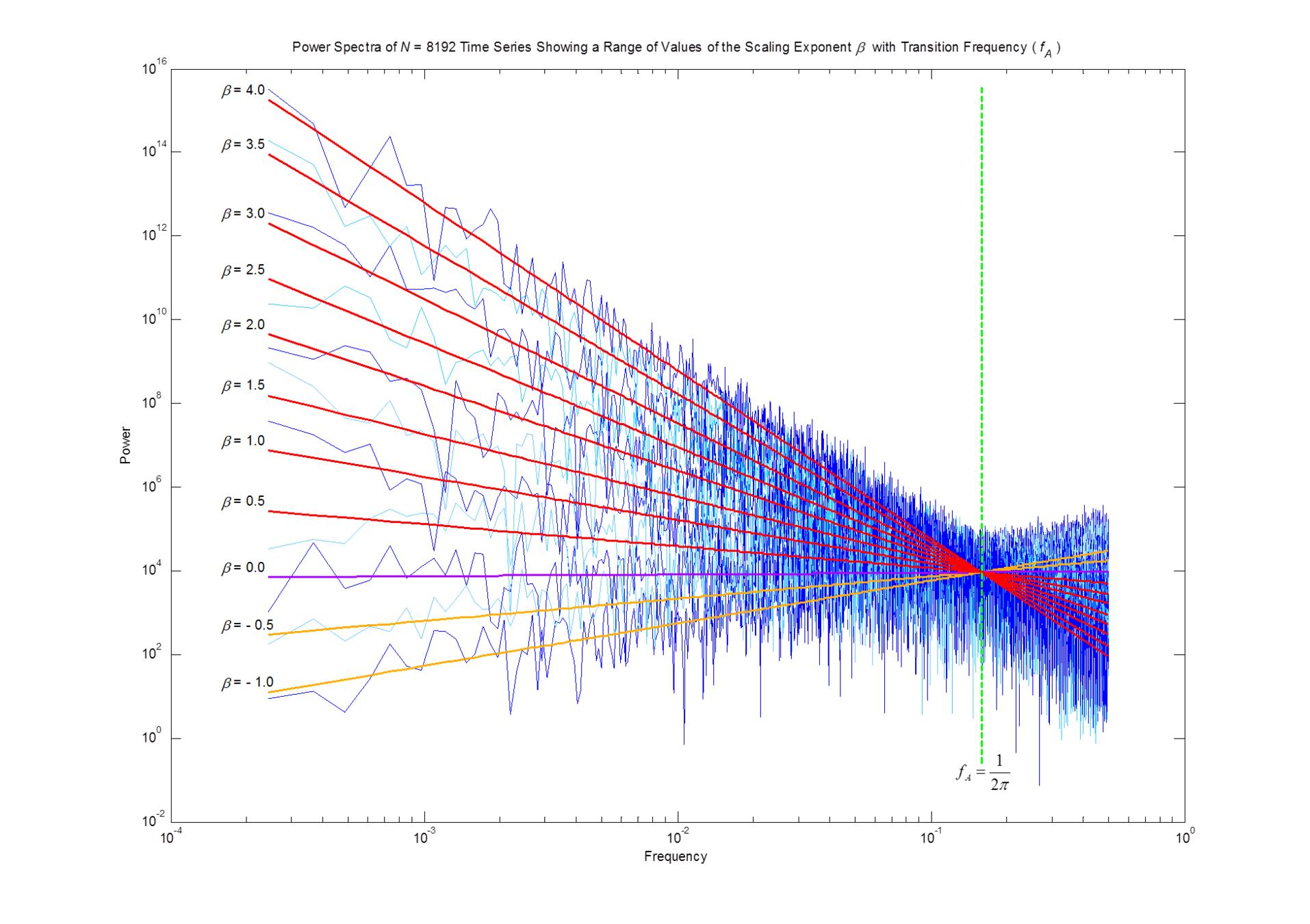
Here, a linear least-squares line fit to the power spectrum of a random white noise signal has a flat slope. If we perform a single integration on this white noise signal, we get what is called a Brownian motion whose power spectrum increases. However, between these two signals, traditional calculus cannot define a signal and we can know nothing about what would happen if the signal was only half-integrated even though fractional integration and fractional differentiation is often found in real-world data.

No calculations of signal between these values.
Traditional Calculus
White Noise
Brownian Motion
# FRACTIONAL CALCULUS
Defining Fractional Calculus

Fractional Calculus as a Calculus of the Operators
Traditional Calculus, demonstrated to the left, is limited in what may be described, filtered, or modeled by the mathematics.
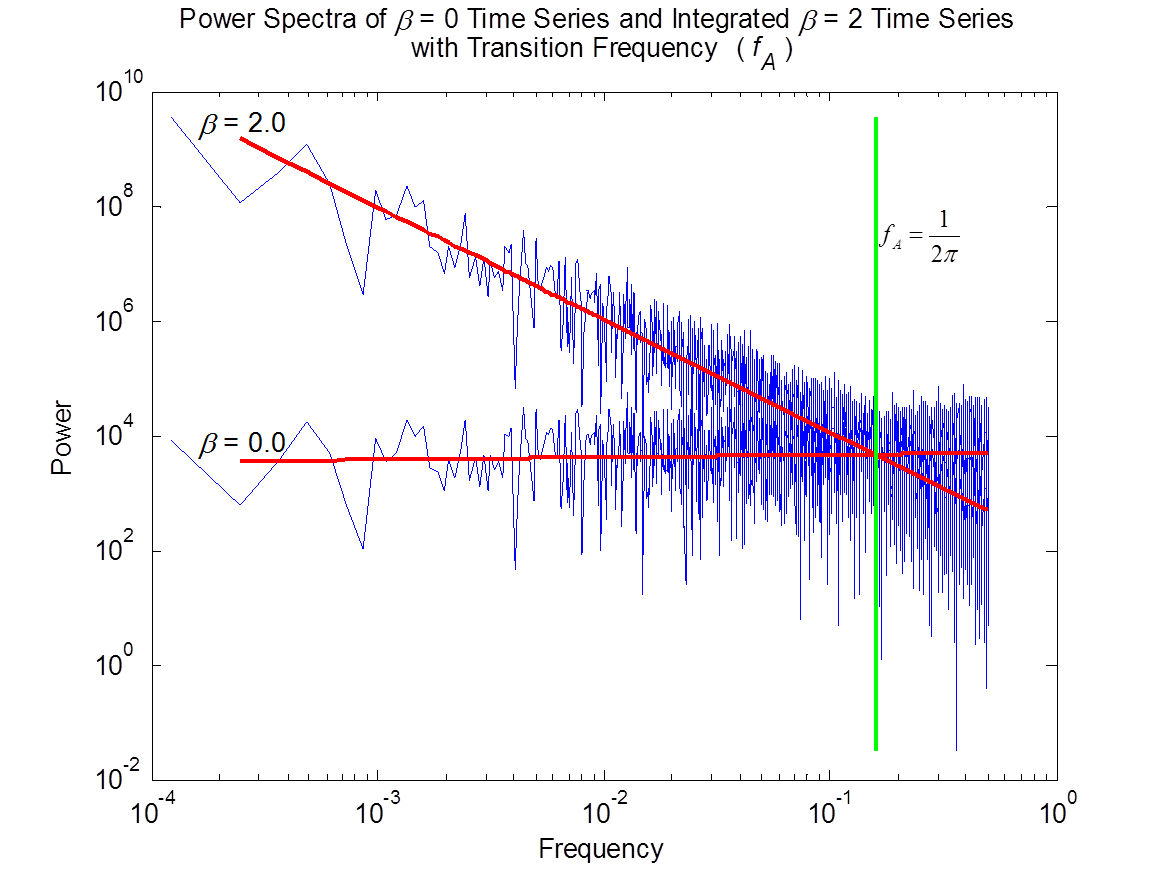
Gaussian White Noise (Differentiation of Brownian Motion):
-
Here, a linear least-squares line fit to the power spectrum of a random white noise signal has a flat slope, also known as a scaling exponent (ß), of ß=0.
Brownian Motion (Integration of Gaussian White Noise):
-
Integration of this same white noise yields a Brownian motion with a power spectrum with a increase in slope or scaling exponent of ß=2.
Scaling Exponent (ß) of Fractional Calculus:
-
The scaling exponent may be used as both a measure of or to perform fractional integration and fractional differentiation through sNRL's patented FSDSP algorithms. In this example, the act of integration of a single, first order integrator changes the slope or scaling exponent of the power spectrum of these signals from ß=0 to ß=2. In contrast, differentiation of this white noise signal would have changed the slope or scaling exponent from ß=0 to ß=-2.
No calculations of signal between these values.
Traditional Calculus

# FRACTIONAL CALCULUS
Fractional Calculus:
- A mathematical framework that extends traditional calculus to allow differentiation and integration of functions at fractional (non-integer) orders, enabling "partial" operations like half-derivatives and half-integrals.
Continuous Change:
- Fractional calculus models processes and changes in a system as continuous rather than discrete steps, providing a smoother transition between states or behaviors
Enhanced Modeling:
- This approach improves our ability to model the dynamic behaviors of complex systems with memory, providing a more flexible and nuanced understanding of these systems.
Examples of Fractional Calculus:
- To the left, we see the effects of fractional integration and fractional differentiation on that same white noise signal. Fractional calculus can capture all transitions between differentiations and integrations.
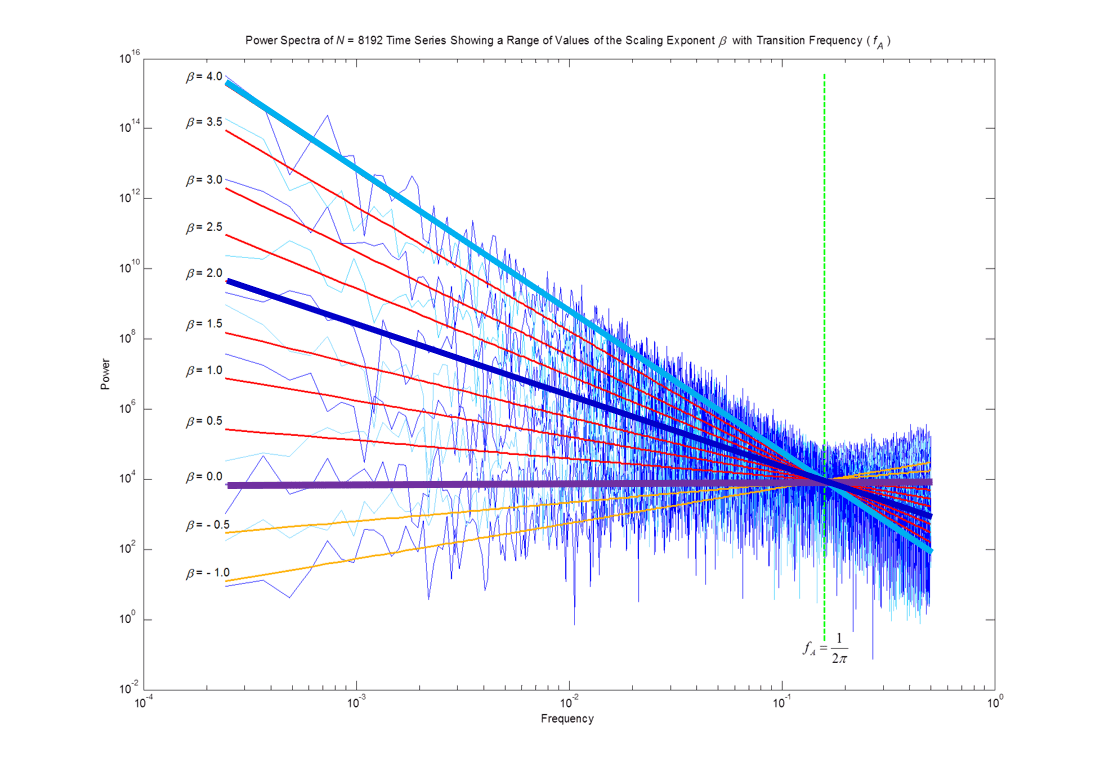
Fractional Calculus fills in the signal area that traditional calculus cannot. While 0.5 increments of ß are shown here, any decimal value may be used resulting in a continuous mathematical model of the signal.
Fractional Calculus
Defining Fractional Calculus (FC)

Fractional Calculus Allows Access to a Broader Mathematical Framework

Defining Fractional Calculus

Fractional Calculus Allows Access to a Broader Mathematical Framework
More Powerful Mathematics through Fractional Calculus:
-
Fractional Calculus allows for the exploration of new mathematical territories that are not accessible with traditional methods. For instance, fractional derivatives or integrals can describe complex behaviors in systems where integer-order derivatives or integrals fail to provide adequate insights or even the ability for fine-scale modeling.
-
As an analogy to a number line, Traditional Calculus is like using only Integers for calculations whereas Fractional Calculus is having access to integers, decimals, and fractions in calculations. The first is an approximation with mathematical artifacts and the second is an exact representation of the answer.
Real-World Signals Are Better Defined via Fractional Calculus:
-
As an example, a half-derivative (ß=1) captures gradual changes in a system, providing a smoother transition between states or behaviors. In contrast, traditional operations tend to create sharp transitions as shown in the previous slide that may not accurately represent real-world phenomena.
-
As shown to the left, Fractional Calculus can capture all transitions between, above, and below 1st (ß=2) and 2nd (ß=4) order integrations or differentiations (ß=-2).
Fractional Calculus
# FRACTIONAL CALCULUS

Defining Fractional Calculus (FC)
# FRACTIONAL CALCULUS

Implications of Fractional Calculus on Computational Algorithms
Efficiency: Fractional calculus enables the application of a single fractional operation (e.g., an all-in-one equation such as a half-derivative) rather than requiring multiple sequential operations (e.g., adding a whole and then subtracting a part).
Reduced Computational Overhead: Performing one operation is generally less computationally intensive than multiple processes, leading to enhanced efficiency and lower energy consumption.
Reduced Error Accumulation: Each operation can introduce potential floating point errors, particularly in simulations, which may accumulate over multiple calculations.
Increased Accuracy: Fewer operations result in less cumulative error, leading to more accurate outcomes in complex system dynamics and real-time processing.
Adaptive Systems: Systems that utilize fractional calculus can dynamically adapt more fluidly to changes in input conditions.
Incorporation of Memory: These systems allow the current state to consider memory and historical data, rather than relying solely on recent inputs.

Fractional Calculus
"Complex phenomena that have often required tortuous explanations, using traditional methods, will eventually be shown to be more naturally described using the fractional calculus." - Bruce West, 2016

# FRACTIONAL CALCULUS UPGRADE
Increase in Number of Published Scientific Articles on FC year to year
Fractional Calculus is the Future

Increase in Patents Issued for Fractional Calculus (FC) Applications
Computing Power and Sensors in Devices are now catching up to the mathematics
Increased Prevalence of Edge Computing needing Dynamic Digital Signal Processing
A New Market is Emerging for Fractional Calculus-Based Technologies

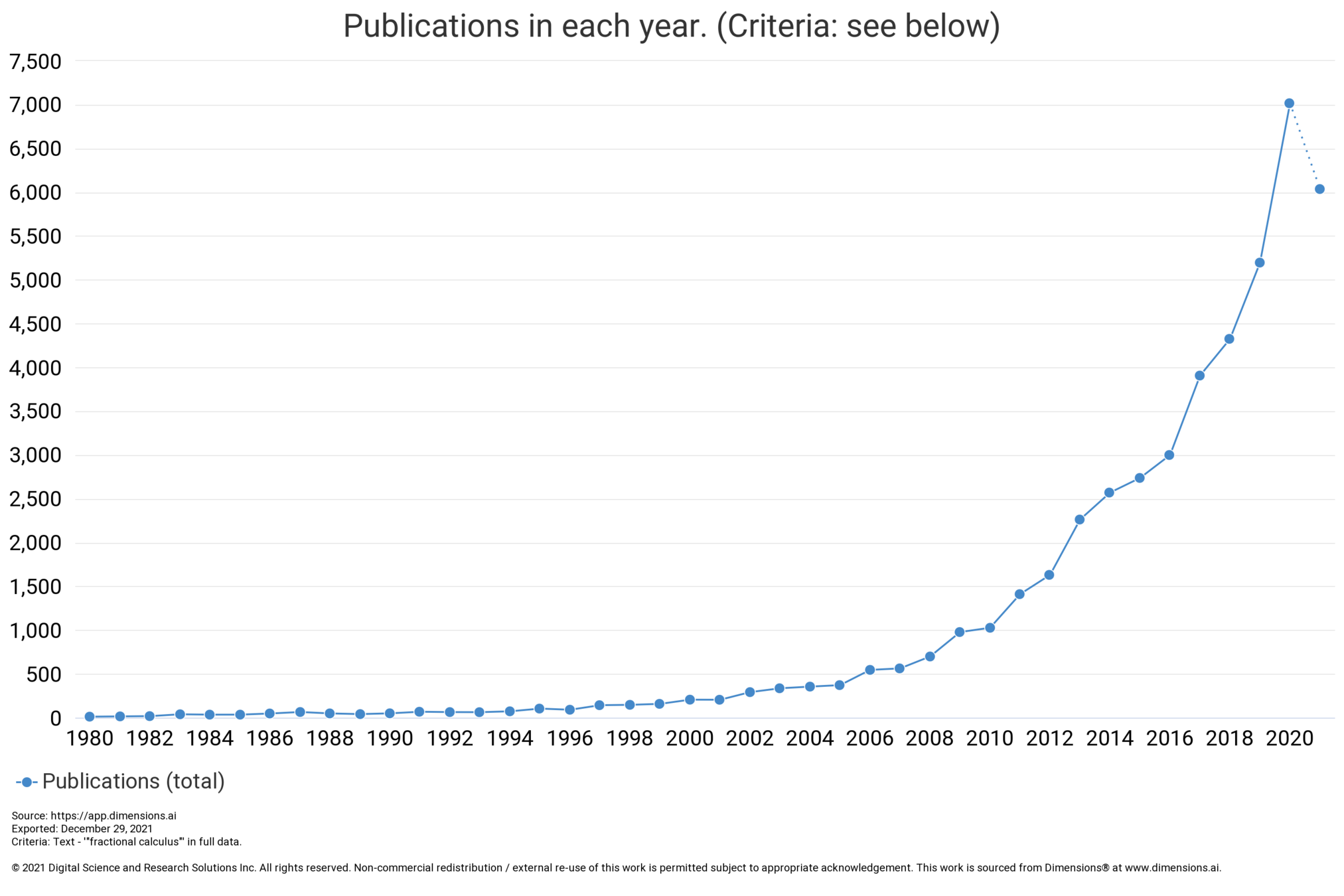
Fractional Calculus Publications Per Year
The potential scale of applications is enormous. Think of how big the market is for calculus-based applications. How much bigger must the market be for Fractional Calculus-based applications?
# FRACTIONAL CALCULUS UPGRADE
Building a Legacy of Innovation in Fractional Calculus

Our Foundational Contribution: Fractional Calculus Research and Development

Strategic Positioning: As pioneers in the field, we are uniquely positioned to leverage our expertise and patents positioning our company to capture and capitalize on emerging market opportunities and drive technological advancements.
Research Foundation: Our journey began over a decade ago in 2005, focusing on the exploration and development of fractional calculus methodologies to modeling complex systems in Geophysics; our work extended to multiple fields.
Utility Patent Milestones: We filed our first patents for fractional calculus algorithms in 2013, showcasing our commitment to innovation and intellectual property in this foundational technology. Our first patent was awarded in 2017 with follow-on patents awarded yearly through 2020.
Depth of Knowledge: Our extensive research has equipped us with a deep understanding of fractional calculus, enabling us to apply it effectively across various applications in signal processing, control systems, and AI.

Fractional Calculus Publications Per Year
Research
Began...
Patents
Filed...
Patents
Awarded.
# sNRL PATENTED TECHNOLOGY
sNRL was Awarded and Holds Foundational Utility Patents

2016

2017

2018

2019

2020

All Patents awarded to and held by sNRL to date collectively generate a foundational platform technology enabling Fractional Calculus Algorithms applicable to all data types and signals.
IP Protection: These Utility Patents consist of Exclusive IP from University Patents (US and International) and cover the methods and algorithms of Fractional Scaling Digital Signal Processing (FSDSP), Fractional Scaling Digital Filters (FSDF), Fractional Order Control Systems (FOCS), and the modeling, filtering, and generation of Standardized Noise, all of which allow or utilize Fractional Calculus expanding the fields of mathematics and digital signal processing. These algorithms, developed by sNRL, may be further enhanced by inclusion within Artificial Intelligence and Deep Learning applications.
4 US Patents Issued (2017, 2018, 2019, and 2020): U.S. Patent 9,740,662, Issued 22AUG2017; U.S. Patent 10,164,609B2, Issued 25DEC2018; U.S. Patent 10,169,293B2, Issued 01JAN2019; U.S. Patent 10,727,813B2, Issued 28JUL2020.
Additional algorithms enhancing the issued patents are already in development and ready to file as provisional patents.
sNRL is Uniquely Positioned to Lead the Field
# sNRL READY FOR LAUNCH


BOOTSTRAPPED BY FOUNDERS
Total Funding to Date: ~ $1M (Sweat Equity, Personal Funding, University Angel Investor)

EXPERIENCED VISIONARY LEADERSHIP
20+ years of relevant experience dedicated to research and development in the field

ROBUST PRODUCT PORTFOLIO USING ONE MASTER LIBRARY BASED ON FC
API (Cloud-based, Internet of Things (IoT)); SDK (Embedded Products, chipsets, Edge Computing)

ONE MASTER LIBRARY SCALES INTO NEARLY ALL INDUSTRIES AND MARKETS
Technology that can benefit from fractional calculus code libraries is limitless and expansive
# FRACTIONAL SCALING DSP (FSDSP)

ONE MASTER LIBRARY: Next-Generation Digital Signal Processing
# FRACTIONAL ORDER CONTROL SYSTEMS (FOCS)
ONE MASTER LIBRARY: Next-Generation Fractional Order Control Systems

- Enhanced Precision: FSDSP enables more accurate modeling and control of dynamic systems through fractional calculus, improving system responsiveness, stability, and recovery from disturbances.
- Improved System Dynamics: By utilizing fractional order derivatives, our technology is less prone to error and allows for finer control over system behavior, leading to smoother transitions, reduced overshoot, increased stability, faster recovery, and quicker target acquisition.
- Adaptive Control Strategies: FSDSP supports the development of adaptive control methods that can dynamically adjust to changing system parameters, enhancing robustness and performance.
- Real-Time Processing: With its advanced fractional calculus capabilities, FSDSP can process complex signals in real-time, enabling immediate adjustments and optimizations in control systems.

# FRACTIONAL ORDER CONTROL SYSTEMS (FOCS)
Understanding Systems, Control Systems, and Fractional Order Control
SYSTEM: A system is a set of interconnected components that work together to achieve a specific objective or function. It can include physical components (machines, sensors, actuators, and controllers), managed processes and interactions, and the relationships between them.
CONTROL SYSTEM: A control system is a collection of hardware and software components designed to manage and regulate the behavior of dynamic processes. It typically includes sensors, actuators, controllers (like microcontrollers or PLCs), and the necessary software algorithms. The system uses feedback loops and signals to adjust inputs to the system or the system itself based on desired outputs, ensuring that the overall system operates as intended in applications such as robotics, manufacturing, and automotive and aerospace engineering.
FRACTIONAL ORDER CONTROL SYSTEM (FOCS): A fractional order control system is an advanced control system that utilizes fractional calculus to manage and regulate dynamic and complex processes. It comprises specialized components, including sensors, actuators, and controllers, along with sophisticated algorithms that implement fractional order control strategies.
BENEFITS OF FOCS: Fractional order control systems provide a more accurate representation of real-world processes and are characterized by their ability to model and respond to a wide range of behaviors through fractional derivatives and integrals, capturing complex dynamics that traditional integer order control systems may overlook. FOCS, applicable across a broad spectrum of technological, medical, and industrial fields, enables more efficient control, providing greater flexibility, improved stability, and enhanced precision and adaptability in performance compared to traditional integer-order control systems.





# FRACTIONAL CALCULUS UPGRADE
ONE MASTER LIBRARY: Impact on Current and Future FC-AI Technologies


Access to Fractional Calculus through ONE MASTER LIBRARY
is Central to the Evolution of Artificial Intelligence
#FSDSP and AIFractional Calculus and Artificial Intelligence
#FSDSP and AI
Artificial Intelligence
meets Fractional Calculus:
sNRL aims to revolutionize the deep learning and AI industry by incorporating fractional calculus into code-libraries tailored for machine-learning and deep-learning applications. While there are libraries and frameworks available for deep learning and AI, no existing solutions specifically focus on integrating fractional calculus algorithms into AI which would effectively change the way AI "thinks" by giving AI a larger "superset" of mathematical tools.
Foundational,
Foothold Technology:
Fractional Calculus AI presents a unique opportunity for sNRL to establish a strong foothold in the market across the increasingly competitive landscape of deep learning and AI. Our goal is to integrate sNRL's patented fractional calculus code-libraries and algorithms into deep learning and artificial intelligence systems, enhancing their performance and pushing the boundaries of what is possible in these rapidly evolving fields to drive innovation.
Improve Existing AI;
Invent Future AI:
By leveraging the power of fractional calculus combined with AI, we aim to revolutionize anomaly detection, predictive modeling, time series analysis, and other critical areas of data analytics. sNRL is both developing code-libraries that integrate our patented fractional calculus DSP algorithms into existing deep learning AI frameworks and also coding our own Fractional Calculus AI frameworks (FC-AI) across multiple fields-of-use.
AI Access to
Fractional Calculus:
These FSDSP and fractional calculus AI code-libraries will allow practitioners to effortlessly incorporate fractional calculus principles into their models thus lowering the bar of entry to use this advanced technology, improving accuracy, solution convergence rates, and efficiency of calculations. Our libraries will support multiple programming languages and frameworks, ensuring compatibility and ease of use for a wide range of users.
Information is all around us, but is often invisible, either imperceptible or the signal is lost in the noise. As a research, development, and innovation laboratory, the sNoise Research Laboratory (sNRL) is leading the way to develop plug and play Fractional Calculus (FC) analytical tools which include advanced digital signal processing libraries, signal-shaping smart filters, advanced machine/deep-learning toolboxes made for AI, and algorithmic mathematical solutions for specific fields-of-use in order to better extract the signal from the noise to reveal the hidden reality of information shaping the technologies of our modern world.
Fractional Calculus and Artificial Intelligence
#FSDSP and AI
Breaking Limitations
of an Exponential Market:
The deep learning and AI market is experiencing exponential growth, with organizations across industries adopting these technologies for improved decision-making, automation, and optimization. However, current algorithms have limitations in capturing long-range dependencies and accurately modeling complex systems. This is where fractional calculus provides a significant advantage, enabling more precise modeling and enhanced performance.
Simplifying
the Complex:
By building fractional calculus code toolboxes for AI, sNRL is providing AI an expanded mathematical library leading to more advanced solutions and the ability to tackle the toughest problems in signal processing. Additionally, the equations of FSDSP are computationally more efficient and can save energy, battery life, and memory used by AI. Our target market includes AI developers, data scientists, research institutions, government, and companies looking to harness the full potential of deep learning and FC-AI.
A New Era
of Intelligent Systems:
By investing in sNRL today, you will be supporting a startup at the forefront of innovation at the intersection of fractional calculus, deep learning, and AI. Together, we will redefine the boundaries of what is possible and pave the way for a new era of intelligent systems. Our patented algorithms and code-libraries have the potential to transform industries across the board, from finance and healthcare to robotics and autonomous systems.
A New Frontier
in Signal Processing:
Through key strategic partnerships and investments, sNRL will better be able to accelerate the development and deployment of our fractional calculus code-libraries enhanced with deep learning capabilities. By joining forces with sNRL, you will be part of an incredible journey to reshape the future of deep learning and AI, unlocking new frontiers in data analysis, modeling, and driving groundbreaking advancements.
Our proprietary algorithms, protected by patents, provide a solid foundation and significant competitive advantage, ensuring the exclusivity and precedence of our cutting-edge technology. We also prioritize continuous research and development, staying ahead of competitors by consistently providing innovative solutions. To use an analogy, sNRL is building the "ChatGPT" and "Shazam" of digital signal processing through fractional calculus embedded within AI (FC-AI) that may identify, amplify, attenuate, filter, reconstruct, denoise, or synthesize any numerical signal with structure.
# SCaLiNG Layered Matrix Network (SLMN)
Layered Matrix Defined:
An organizational framework where components (specialized layers) operate across multiple levels of specialization and interaction, with each layer representing a distinct function or domain of expertise. In this model, resources (such as data, algorithms, and processing units) are accountable to various supervisory nodes (domain groups) and rely on specialized domain expert AI subsystems to deliver their intended functions. This mirrors the complexity of cognitive processes found in biological systems, where different regions of the brain collaborate to perform tasks and solve problems.
Benefits of the Layered Matrix Network:
- Interdisciplinary Collaboration: Different specialized AI modules work both independently and together, processing and passing data, similar to distinct areas of the brain collaborating to process information.
- Dynamic Adaptability: The system can scale efficiently, leveraging expertise from various layers to adapt to changing data and requirements. Continuous engagement between layers facilitates real-time adaptation and optimization.
- Multidimensional Accountability: Each layer can be managed independently while remaining linked to a broader network, ensuring clear responsibilities and effective utilization of specialized knowledge.
- Centralized Control: A central Orchestration Neural Engine (ONE) manages both the supervisory domain groups and subsystem domain experts, ensuring cohesive integration and alignment across all layers.
Summary:
The SCaLiNG Layered Matrix Network (SLMN) embodies a robust and adaptable approach to AI development, reflecting the interconnected and hierarchical nature of cognitive processes in the brain while leveraging fractional calculus for superior performance where others may falter.

SCaLiNG Layered Matrix Network (SLMN)



# SCaLiNG Layered Matrix Network (SLMN)
Overview:
-
SLMN is a revolutionary AI architecture inspired by the hierarchical structure of the human brain, designed to facilitate complex reasoning and dynamic learning.
-
The system comprises the Orchestration Neural Engine (ONE) as the central coordinator, optimizing the activities of a network of specialized expert AIs that tackle distinct tasks across various domains.
Architecture:
-
Orchestration Neural Engine (ONE): Resembling the cerebrum, ONE coordinates and optimizes the performance of the expert AIs, adapting to real-time changes using fractional calculus for predictive analysis.
-
Specialized Intelligence Matrix (SIM): A complex matrix of multiple specialized expert AIs focused on distinct domains (e.g., borehole telemetry, medical diagnostics, audio analysis), each simulating the higher-order processing functions of the human neocortex.
-
COre Management Administrator (COMA): Resembling the Brainstem in the regulation of vital functions, COMA manages foundational operations such as data preprocessing and system health monitoring, ensuring reliability and efficiency.
-
Memory Integration System Topology (MIST): Resembling the Hippocampus, facilitates memory formation, integration, and retrieval, utilizing historical data for informed decision-making, supported by fractional calculus for modeling memory dynamics.
-
Fractional Calculus Integration:
-
Utilized throughout the SLMN architecture, fractional calculus enhances the ability to process complex data, model dynamic systems, and support advanced reasoning capabilities across all components.

SCaLiNG Layered Matrix Network (SLMN)




# SCaLiNG Layered Matrix Network (SLMN)
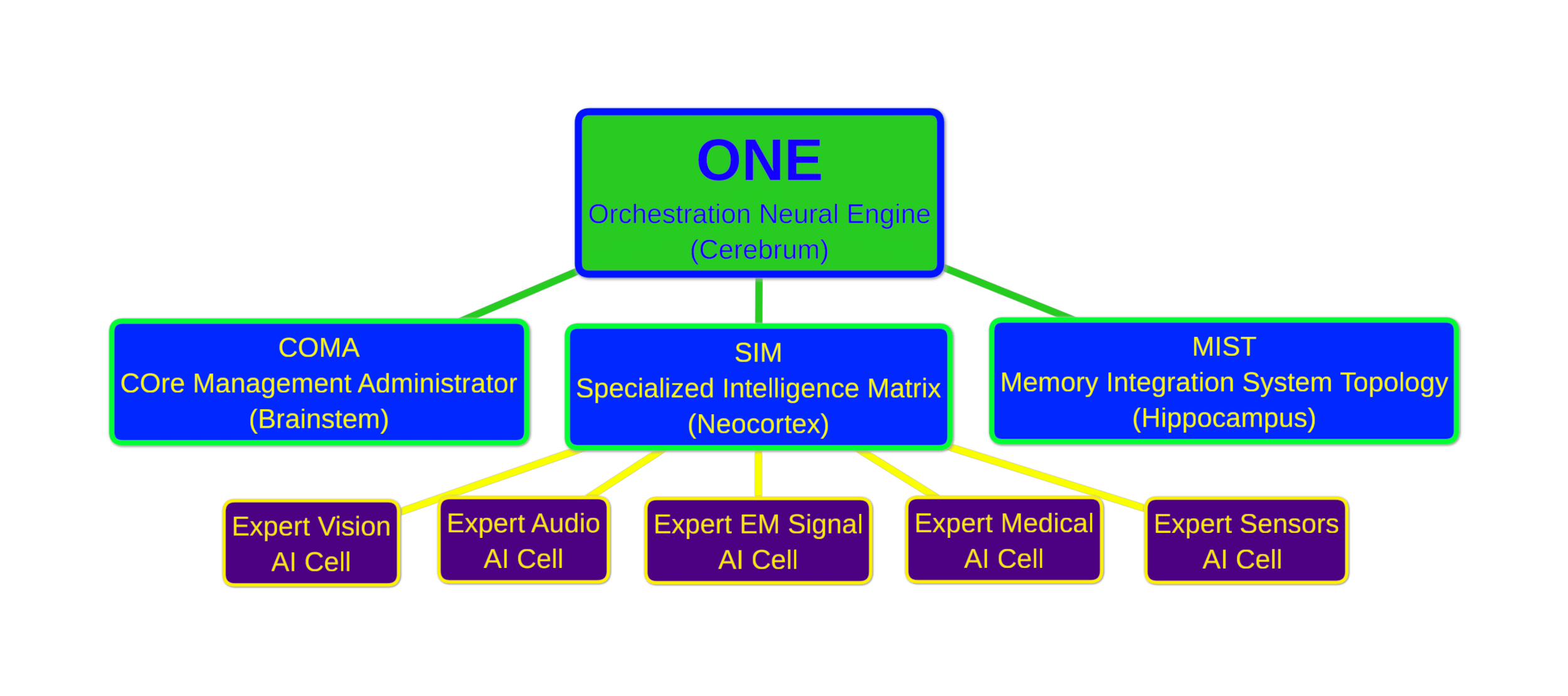

# SCaLiNG Layered Matrix Network (SLMN)Expert AI Example in Medicine:
-
Medical Signal Analysis: An AI trained to analyze heart rhythms and detect anomalies, utilizing fractional calculus to improve signal clarity and reduce noise, enabling more accurate diagnostics.
-
Neuroactivity Monitoring: A dedicated AI interpreting brainwave patterns, employing fractional calculus to model dynamic changes over time, aiding early detection of conditions like Alzheimer's.
-
Audio Processing: An AI focused on speech patterns, using fractional calculus to filter and adjust audio signals in real-time, from enhancing clarity for hearing aids to identifying voice signatures related to medical conditions like Parkinson's.
Real-World Impact:
-
Expert AIs developed using sNRL's fractional calculus libraries are expected to significantly improve healthcare diagnostics, enhance decision-making processes, and contribute to better patient outcomes through advanced analytical capabilities.
SLMN: Expert AIs and Their Applications



SLMN: Orchestration Neural Engine (ONE)
# SCaLiNG Layered Matrix Network (SLMN)


Orchestration Neural Engine (ONE):
Role:
-
ONE functions as the central coordinator, integrating outputs from expert AIs and managing system-wide operations, similar to the cerebrum's role in higher cognitive functions such as decision-making, information synthesis, problem-solving, and complex reasoning. By this measure, ONE integrates data from various layers and diverse types of information to form a cohesive understanding.
-
Utilizes fractional calculus to optimize planning and execution of multi-step processes by analyzing historical performance data and predicting ideal outcomes.
Capabilities:
-
Responsible for adapting strategies based on real-time feedback, ONE mimics the brain’s ability to learn from experience and adjust actions accordingly, employing fractional calculus to model and anticipate changes in system dynamics.
-
Integrates the functionalities of COMA, SIM, and MIST, ensuring seamless communication and collaboration among these components to enhance overall system performance.
-
Facilitates dynamic resource allocation, allowing the system to prioritize tasks and allocate processing power where it is most needed, improving efficiency and responsiveness.
-
Monitors system health and performance metrics, proactively identifying potential issues and making adjustments to maintain optimal operation.

SLMN: Layered Matrix, Core Operations, and Memory Integration
# SCaLiNG Layered Matrix Network (SLMN)
COre Management Administrator (COMA):
-
Resembles the brainstem, managing essential tasks like data preprocessing and system health monitoring, akin to the brain's regulation of vital functions such as heart rate and respiration.
-
Fractional calculus ensures efficient processing of incoming data streams, minimizing latency and ensuring reliability.
Specialized Intelligence Matrix (SIM):
-
Functions similarly to the neocortex as an interconnected system of specialized functions where fractional calculus-based expert AIs analyze complex data and perform specific tasks.
Memory Integration System Topology (MIST):
-
Illustrates how the AI retains and leverages historical data for informed decision-making, analogous to how the human hippocampus facilitates memory formation, integration, and retrieval.
-
Employs fractional calculus to model memory decay and retrieval processes, enabling the AI to adapt its responses based on the relevance and recency of past states and interactions, thereby enhancing memory dynamics and improving overall learning processes.
-
Incorporates topological analysis, enhanced by fractional calculus, to understand structural brain network patterns and examine how connectivity influences cognitive processes and memory organization.
-
Supports modeling of topological fluctuations related to network stability using fractional calculus, which is critical for understanding how these fluctuations affect, disrupt, or alter overall system behavior.
-
Utilizes topological metrics derived through fractional calculus to analyze connectivity patterns within the neural network, providing insights into the efficiency and robustness of communication pathways that support cognitive functions as they evolve over time.





Advancing AI Beyond Pattern Matching:
-
SLMN leverages fractional calculus to enable complex reasoning, allowing for sophisticated interactions that go beyond simple pattern matching and recognition.
-
The integration of fuzzy logic enhances the AI's adaptability, enabling it to navigate uncertainty and make nuanced decisions based on incomplete or ambiguous data.
Reasoning Capabilities:
-
By mimicking the hierarchical and interconnected nature of the human brain, SLMN may simulate higher-order thinking processes, allowing it to understand context, predict outcomes, and adapt to new information in real-time.
-
This architecture supports dynamic learning and real-time adaptation, which are critical for applications requiring not just reactive responses but proactive decision-making and innovative problem-solving, all enhanced by the mathematical rigor of fractional calculus.
Transformative Potential of SLMN:
-
With its innovative architecture and advanced mathematical modeling, SLMN is positioned to redefine the capabilities of AI systems, demonstrating enhanced reasoning and adaptability that could set a new benchmark in the industry.
-
By harnessing these features, SLMN aims to establish a new standard for intelligent decision-making, addressing the growing demand for AI that can perform complex reasoning and effectively tackle real-world challenges.
-
Leveraging dynamic learning and robust multi-modal processing, SLMN stands to enhance overall performance, reinforcing its role as a transformative force in the future of artificial intelligence.

SLMN: A New Benchmark for the Future of AI


# SCaLiNG Layered Matrix Network (SLMN)
The Market is at the Threshold of Exponential Growth
# 21st CENTURY SOLUTIONS

Applications that were once only in the lab now have massive commercial applications, especially when Fractional Calculus is Integrated into Artificial Intelligence Systems.
Fractional Calculus, although first introduced 300 years ago, is an emerging field of mathematics and applied scientific discipline which has accelerated in this past decade as computing power and sensor technologies have caught up with the mathematics. Fractional Calculus has vast and extensive applications in all related fields of science and engineering.
21st century problems
require
21st century solutions
# sNRL SDK, API, FSDSP CHIPSETS




Application Programming Interface (API)
- Cloud-based Fractional Calculus AI
- Data Server and FSDSP Processor
- Internet of Things (IoT)
- The "ChatGPT" of Signal Processing
Software Development Kit (SDK)
- Embedded Products
- Edge Computing
- Microcontrollers
- FSDSP Chipsets
Fractional Scaling Digital Signal Processing (FSDSP) Chip/Microcontroller
- Incorporates FSDSP/Fractional Calculus
- May be programmed through SDK
- May interface with API
Licensing Vehicle:
Revenue Generation
Product Portfolio:
FC Toolkits/AI Engine

ONE MASTER LIBRARY Generates Revenue through Product Portfolio
sNRL POISED FOR EXPONENTIAL GROWTH
# sNRLTECH MARKETPLACE
Write Once...
Run Anywhere:
Expect nonlinear or exponential response out of proportion to our entry into market. Once patented algorithms with AI are integrated into an API and SDK, codebase may be run on multiple types of datasets or deployed via multiple types of microcontrollers or chipsets. Design and maintenance of front-ends for specific fields of use ensure compatibility. Additional feature sets, analysis, and use cases continuously being developed and patented.
Standardized
Algorithm Search Engine:
Currently, one cannot just Google an algorithm for quick implementation. The sNRLTECH codebase provides a search engine for standardized algorithms and fractional order control system applications. Essentially, the API and SDK provide plug and play capability for sensors to use advanced digital signal processing combined with AI for rapid incorporation into prototypes and licensing of any proprietary algorithms.
Clearinghouse for
Algorithmic-based Tech:
Although focused on Fractional Calculus and AI, the API and SDK may become a searchable database of proprietary algorithms that may be licensed with a percent of the licensing fee to sNRL for maintaining and licensing these algorithms. This would also create a market for algorithms at Universities that otherwise go unlicensed making them more accessible. Scientists could add their own proprietary data or algorithms to the database and share in licensing fees.
Modularized Building
Block Architecture:
The sNRLTECH API and SDK creates an architectural framework of modularized building block algorithms that seamlessly link together so that any signal is processed correctly with minimal effort. An import tool utilizing deep learning and AI would serve to orientate the input data correctly for the algorithms based on the type of data to be processed. Rapid generation of FSDSP filters are obtained through a Data Equalizer GUI.
sNRLTECH: A fractional scaling digital signal processing SDK, API, chipset integration, user-interface, and licensing platform utilizing sNRL's patented advanced mathematical algorithms based on fractional calculus further enhanced through deep learning and AI to filter, model, reconstruct, and synthesize digital signals from a variety of data measurements and sources such as audio, radio, video, industrial, SONAR, RADAR, and medical sensors.
# sNRLTECH LICENSING VEHICLE




Lowers the bar of entry for anyone to use the power of fractional calculus and AI from the student to the advanced signals processing engineer, mathematician, or scientist (e.g., data equalizer)
Provides a Vehicle to License patented FSDSP technology enhanced with AI to a variety of industries and for use embedded in products automatically setting up licenses and billing according to use
Provides metrics of use and scaling so that licenses may be monitored and appropriately priced per data processed, field of use, and/or embedded product or FSDSP microcontroller or FSDSP Chipset
Potential to also create dedicated user-based community in which scientists, engineers, and programmers may develop add-ons, specific front-ends for abstract data sets, or share data and settings driving engagement and licensing of sNRL technology

Revenue Generation through Licensing of Product Portfolio
Licensing Vehicle: sNRLTECH.com
- Enterprise SDK and API with FC-AI Engine
- Application-centric Microservices
- Multiple Fields of Use/Front-ends per data type
- Multiple License Types (data type/processed)
- Hosted AWS cloud for scalability
- Can be loaded onto hardware or embedded in chips
- Provides automatic sign-up, billing, license checkout
- Provides Metrics of use, data processed, and scaling
- Lowers the bar of entry for anyone to use FC-AI
- Dedicated User-Based Community and Marketplace
# VALIDATED, PROVEN TECHNOLOGY
Validation and Proof-Of-Concept Confirmations

# EM BOREHOLE TELEMETRY
Electromagnetic Borehole Telemetry
FSDSP provides a solution to solve the problem of in-band noise transmission errors in an Electromagnetic (EM) Borehole Telemetry System of land-based drill rigs that provide EM telemetry from the smart drill in the borehole to the drill rig at the surface using extremely low frequencies (<=12Hz). Of note, all land-based rigs with EM Borehole Telemetry systems have the same in-band noise problems so the market extends to all operators of such rigs and also Ground-Penetrating RADAR systems.

Evaluation of FSDSP by Engineers at an Oil Field Services Company that supplied the data showed that FSDSP did increase the signal-to-noise ratio (SNR), accuracy of symbol decoding, and recognition of EM Borehole Telemetry data when compared to the traditional digital signal processing methods currently used by the same Oil Field Services Company.
The increased accuracy of FSDSP will significantly reduce re-boring (at a estimated cost of $1-2m per borehole, on average) leading to more efficient operations.
As a result of this validation and proof-of-concept application of FSDSP to telemetry data, the management of the Oil Field Services Company requested an outline of licensing terms of Fractional Scaling Digital Signal Processing from sNRL for a Multi-Year, Multi-Use License with Oil Field Exclusivity. Primarily, with this license, sNRL's FSDSP technology would be utilized through the API and SDK to improve upon current Electromagnetic Borehole Telemetry signal processing in land-based drill rigs.

# FSDSP AUDIO
Audio/Data Signal Processing x100
Multiple Music and Audio Signal Processing Companies and Advanced Military Technology Developers have expressed interest in licensing the FSDSP SDK or API once developed

Audio Signal Processing Applications
- Voice Synthesis, Extraction, Compression, and Conversion
- Music and Instrument Synthesis and Hybridization, Speaker Emulation
- Noise Reduction, Isolation, Selective Removal of Individual Frequencies
- 3D Audio, Binaural Audio, Directional Filtering, Directional Enhancement
- Enhanced or Augmented Reality Hearing, OTC Hearing Aids, Hearing Emulation
FSDSP allows for unparalleled audio signal processing capabilities with the ability to access and adjust every single individual frequency, in both magnitude and/or phase, and time element of each frequency (i.e., forward, backward, or pausing individual frequencies) without affecting or interfering with adjacent frequencies.





# FSDSP RADAR/SONAR
RADAR/SONAR Signal Processing x100
SONAR and RADAR processing applications are immense
- Potential to develop new Synthetic Aperture RADAR (SAR) ultra-high resolution FSDSP Doppler Filter Banks
- Improved Resolution of Side-Scan and Multi-beam SONAR Imagery
- Improved SNR and Clutter Suppression of Noise in RADAR and SONAR
- Enhancement of Individual Frequencies revealing otherwise Stealth Signatures
- Applications: Aircraft, Autonomous Vehicles, Drones, Weather, Satellites, Shipboard, Sensors, and more

# FSDSP MEDICAL AND TELEMEDICINE
High Value Medical and Telemedicine Applications
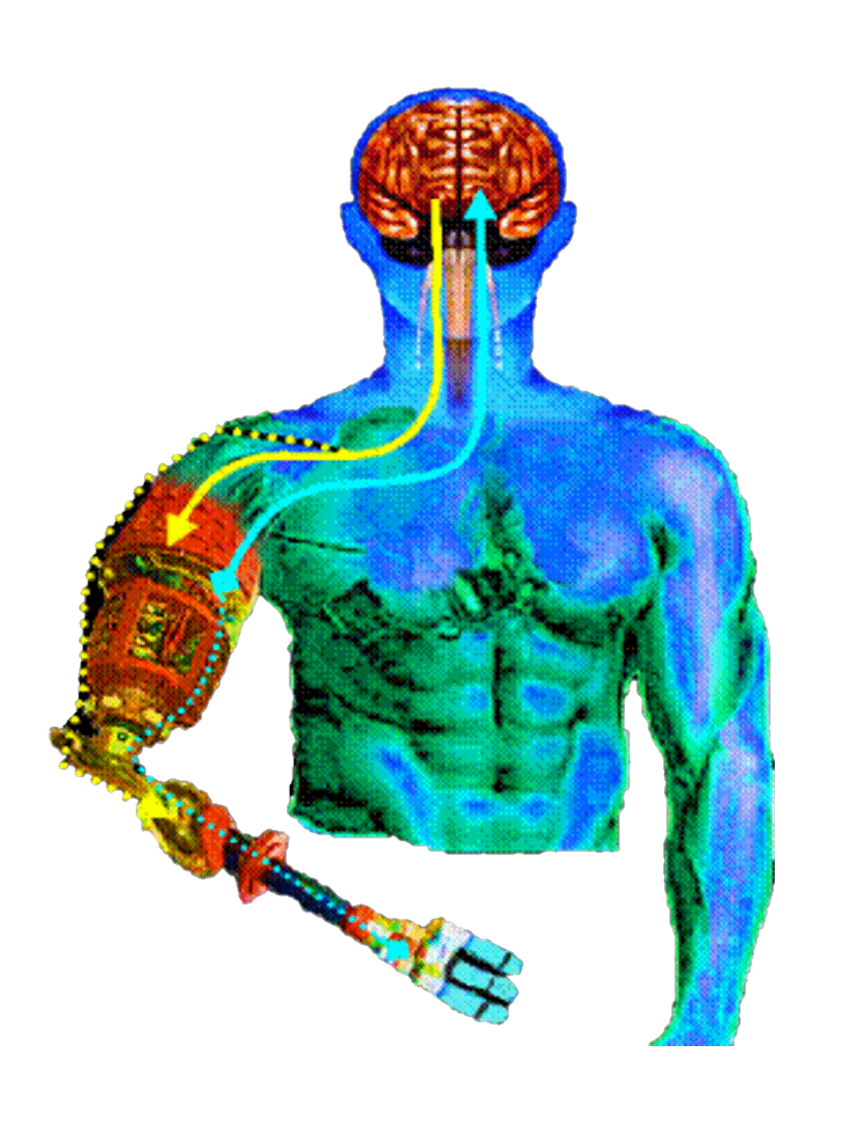
FSDSP allows for the digitization of brain and nervous system signals through the development of advanced signal processing algorithms for a Brain-Machine Interface or bioelectrical interface. For example, FSDSP offers potential enhancements of the bioelectrical interface stemming from improvements in sensor and filter design which may yield significant increases the functionality of bionic neuroprosthetics. This allows for more accurate identification and interpretation of bioelectrical signals, such as augmenting the signal passed through a spinal cord bridge to repair paralysis. Additionally, FSDSP allows for EEG brain wave isolation and extraction, analysis, and identification/modeling of brain and nervous system activity leading to highly accurate mathematical, computationally-based methods to quantitatively diagnose neurological disorders.

FSDSP provides the capability to address characteristics of human information processing, enhance the collection, analysis, and filtering of brain, electrical, and nervous system signals, and allows for the development of more accurate and advanced sensors used to record electrical activity, such as EEG data, through enhanced filtering equations.
Sample of FSDSP Medical Applications:
- Spectroscopy
- Speech Pathology
- Biomedical Imaging (MRI)
- Genetics
- Neuroscience / Neuroengineering
- Robotics / Bionics
- First Responders
- Telemedicine / Sensors
- Directed Energy Therapy
- Cardiology
EKG Heart Rate, Breathing Extraction, and Analysis from Video
Original Video*
FSDSP Video*
* Original Video - MIT Labs; * FSDSP Video - sNoise Research Laboratory
# FSDSP SOFTWARE-DEFINED-RADIO
FSDSP Software-Defined-Radio to solve Electromagnetic Spectrum Access
FSDSP offers a mathematical solution to increase spectrum capacity to address the Spectrum Congestion Problem, allowing both more usable frequency bands (more subchannels) per allocated bandwidth and also more devices per channel (more frequencies available to hop between). FSDSP can be used to create extremely sharp digital filters that can isolate bands of frequencies without interfering with and independent of adjacent frequencies (e.g., HD multiplexing).

FSDSP offers the potential to increase spectrum capacity by more efficiently splitting up access to the physical spectrum through FSDSP filters. Thus, more information, stations, or channels may be added to current Spectrum Allocations without loss of fidelity resulting in an increase in the performance of radio digital signal applications or related devices ranging from Software-Defined Radio (SDR), Fiber Optics, IoT, and telecommunications, to Bluetooth, Wi-Fi, and video (e.g., streaming) or radio broadcasting.

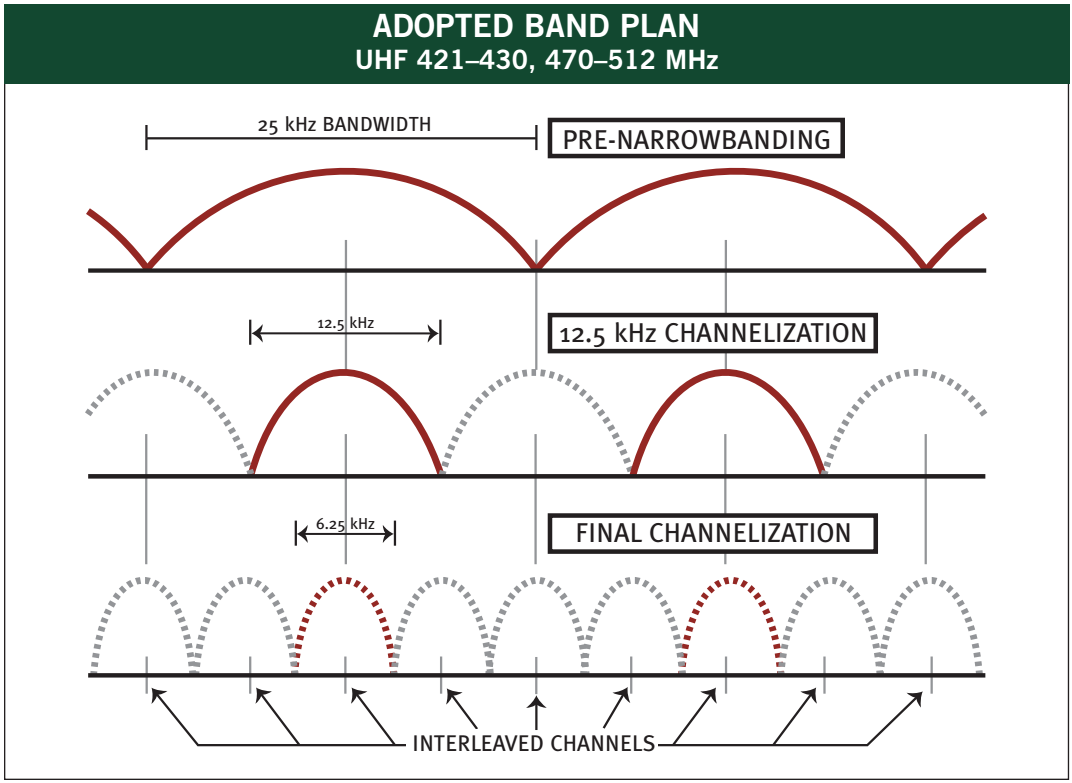
FCC Narrowbanding Mandate - Traditional Filters
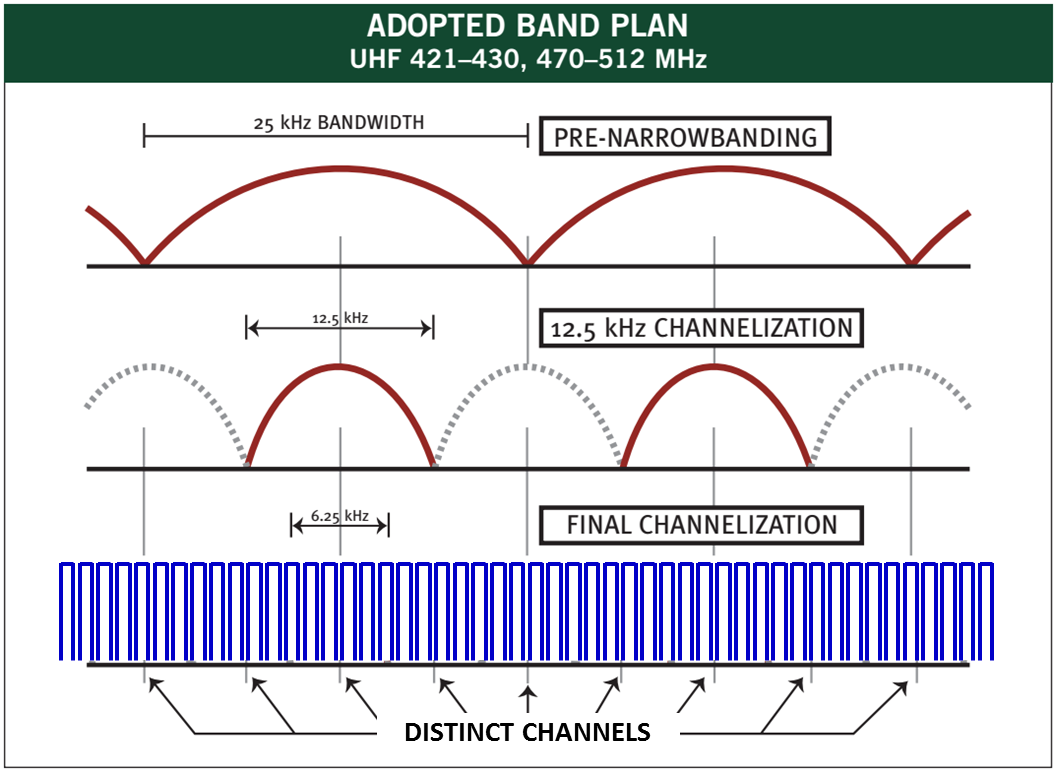
FCC Narrowbanding Mandate - FSDSP Filters
With improved fractional scaling digital filters for tuning and isolating a signal from the interference of adjacent frequencies, FSDSP extends the usable reception range leading to fewer dropped calls and less noise in radio signals.
Encryption of Radio Signals within Noise (Military-Tactical Software Defined Radios) is also possible through FSDSP offering the ability to embed high resolution signals in what appears to be random noise or any other signal over open airwaves.
# FSDSP MACHINE LEARNING - AI
MACHINE/DEEP LEARNING AND ARTIFICIAL INTELLIGENCE WITH FSDSP
FSDSP, utilizing Fractional Calculus, provides an extensive mathematical toolset to enhance Machine/Deep Learning (ML) and Artificial Intelligence (AI) Algorithms for Feature/Pattern Detection, Extraction, and Synthesis/Reconstruction of a signal.
FSDSP captures the scaling and frequency behavior of complex time series, systems, and structured data within equations and can yield statistically identical simulations and models of these data sets to allow you to "animate", extrapolate, filter, simulate, and understand these systems giving us the ability to determine "What’s inside the black box?" and how the ML algorithms or AI came to a solution.

FSDSP also allows for the development of more efficient and accurate ML algorithms for signal processing as there are fewer parameters necessary within the FSDSP equations that would need to be modified or modeled by a ML system when compared to traditional filters and systems allowing AI to come to a solution faster yet more accurately.
This is why FSDSP can emulate natural signals such as a realistic voice as the equations of FSDSP and mathematics of Fractional Calculus more accurately represent how nature works and may bring us closer to a true, cognitively functioning AI.


# sNRL PROOF OF CONCEPTSFSDSP EXCEEDS THE STATE-OF-THE-ART INDUSTRY STANDARD



sNRL CASE STUDY:
Electromagnetic Borehole Telemetry
An environmental filtering effect occurs as the EM borehole telemetry signal passes through the bedrock on the way to the receiver in the drill rig which distorts a range of frequencies within the signal. The source of the in-band noise that corrupts the signal is generated from a combination of through-ground transmission and subsequent attenuation due to various densities and compositions of the bedrock as well as interference in the rig equipment itself on the surface.
sNRL was contacted to solve this in-band noise problem by an Oil-Filed Services company and analyzed over 100 EM Borehole Telemetry datasets provided by the company. Based on sNRL's results, FSDSP allows for the generation of a dynamic model of this environmental filtering effect and the subsequent creation of an anti-distortion filter. This FSDSP anti-distortion filter is applied to the signal received at the drill rig to remove in-band noise and correct for the environmental filtering effects of the bedrock to reconstruct the telemetry signal. In this way, through FSDSP, the signal received from the drill is restored as if the signal passed through the bedrock with very limited interference.
Overall, the focused application of FSDSP to EM Borehole Telemetry elevates the clarity of the signal and provides greater ability to decode messages embedded in the signal significantly improving cost savings.
# sNRL PROOF OF CONCEPTS
FSDSP EXCEEDS THE STATE-OF-THE-ART INDUSTRY STANDARD
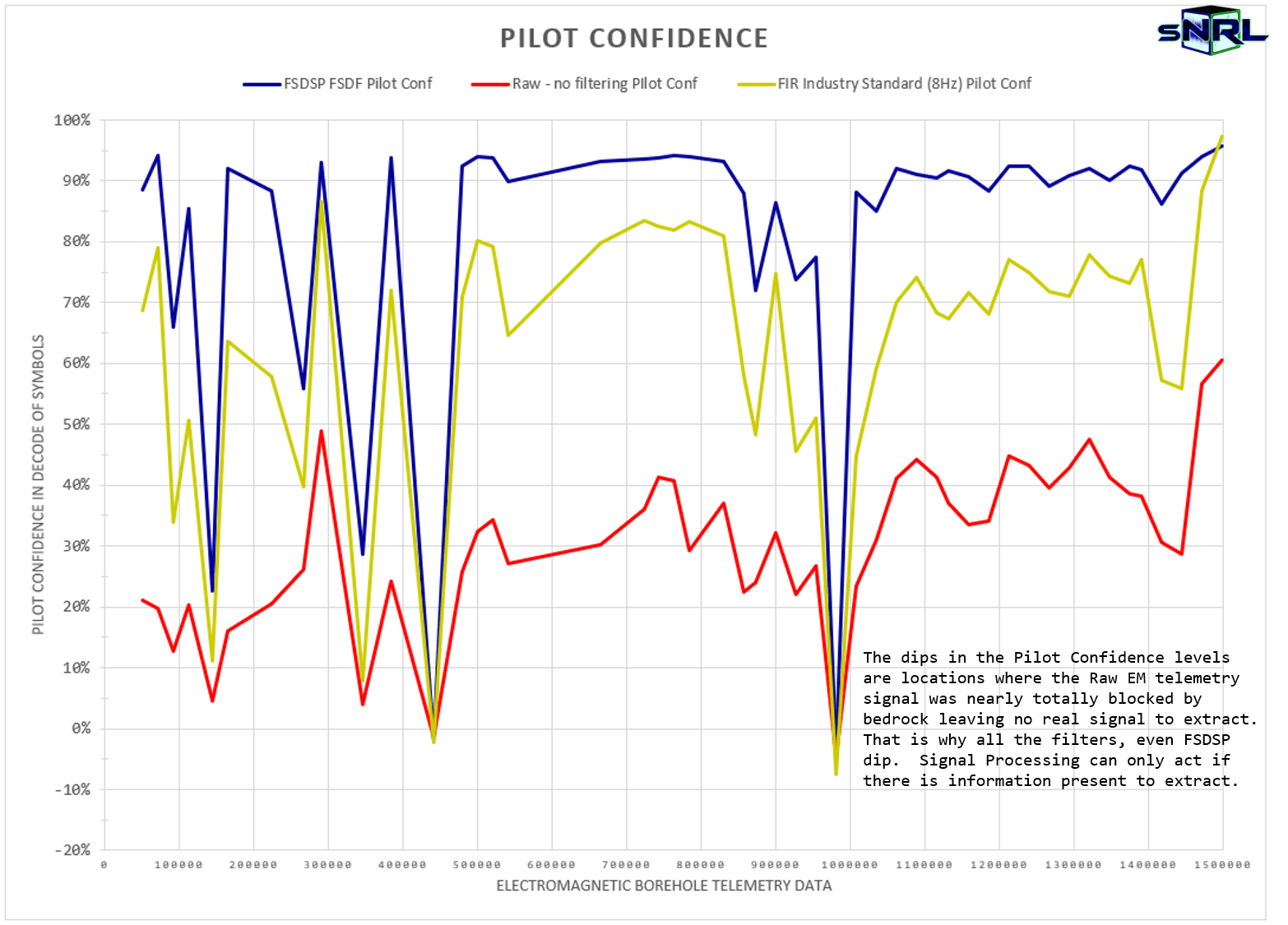
Electromagnetic Borehole Telemetry
Pilot Confidence in the accuracy of the Raw EM telemetry signal received at the drill rig with no correction was around 30% on average. FIR Industry standard signal processing increased the Pilot Confidence to around 63% on average. FSDSP based on a fractional calculus approach significantly increased the Pilot Confidence to around or above 90% on average.
Raw EM Telemetry is the Pilot Confidence of the signal received at the drill rig with in-band noise after having been distorted by the bedrock with no post-signal processing.
FIR Industry Standard is the Pilot Confidence of the signal after the application of traditional post-signal processing filters performed by the Oil-field Services company to attempt to correct for in-band noise in the Raw telemetry signal.
FSDSP FSDF is the Pilot Confidence of the signal after the application of the fractional calculus based signal processing anti-distortion filter applied to the Raw telemetry signal.
# sNRL PROOF OF CONCEPTS
FSDSP EXCEEDS THE STATE-OF-THE-ART INDUSTRY STANDARD

Electromagnetic Borehole Telemetry
The Signal-to-Noise Ratio (SNR) in decibels (dB) is compared. The SNR of the Raw EM telemetry signal received at the drill rig with no correction was mainly negative and well below the noise floor resulting in more noise than signal.
The SNR of the FIR Industry standard signal processing increased the SNR in some areas where signal was present yet still could not decode all regions, especially as the data count increased which may also be thought of as a proxy for time/distance in that the drill bit is further from the receiver later in the data set. The SNR of the FIR processed data passes below the noise floor later in the data set.
FSDSP FSDF based on a fractional calculus approach significantly improved the SNR of the data and was able to recover data previously unrecoverable using traditional signal processing. The SNR was always well above the noise floor when a signal was present.
# sNRL PROOF OF CONCEPTS

FSDSP EXCEEDS THE STATE-OF-THE-ART INDUSTRY STANDARD

FSDSP as the Solution for EM Borehole Telemetry
Results of over 100 data sets processed with FSDSP by sNRL were evaluated by engineers at an Oil-Field Services Company that supplied the data. The engineers found that FSDSP significantly increased the signal-to-noise ratio (SNR), improved the accuracy of symbol decoding and pilot confidence, and enhanced the recognition of EM Borehole Telemetry data when compared to the traditional digital signal processing methods currently in use by the company.
Additionally, the FSDSP Anti-Distortion Filter can be constructed on-the-fly as an adaptive filter in real-time drilling operations. Thus, as the drill bit moves, at specific intervals, the FSDSP Anti-Distortion filter may be continuously reconstructed algorithmically to adjust for changing conditions of the bedrock since it is expected that the attenuation of frequencies by natural bedrock is dynamic based on density and composition of the bedrock and the location and distance from transmitter to receiver. Constant interrogation of the environment would ensure the most accurate real-time filter for frequency restoration and carrier extraction significantly reducing errors in the EM Borehole Telemetry signal.
# sNRL PROOF OF CONCEPTS
FSDSP EXCEEDS THE STATE-OF-THE-ART INDUSTRY STANDARD

Market Effect of FSDSP on EM Borehole Telemetry
The EM Telemetry signal carries symbols and messages regarding the state of the drill, the composition of the substrate that is being drilled, and the location and direction of movement. This is why errors in message decoding during drill operations often result the drill trajectory going off course and the need to correct the course of the drill by re-boring an entirely new well. Re-boring a well involves dismantling, moving, and rebuilding the land-based drill rig at a estimated cost of $1M to $2M per borehole, on average, so reduction of errors is essential for reduced costs to the operator.
Of note, all land-based rigs with EM Borehole Telemetry systems have similar in-band noise problems so the market for a FSDSP solution extends to all operators of such rigs and also Ground-Penetrating RADAR systems. The increased accuracy of FSDSP significantly reduces errors and re-boring leading to more efficient operations.
As a result of this validation and proof-of-concept application of FSDSP to telemetry data, the management of the Oil-Filed Services Company requested an outline of licensing terms of Fractional Scaling Digital Signal Processing from sNRL for a Multi-Year, Multi-Use License of FSDSP with Oil Field Exclusivity. Primarily, with this license, sNRL's FSDSP technology would be utilized through the API and SDK to improve upon current Electromagnetic Borehole Telemetry signal processing in land-based drill rigs.
# sNRL PROOF OF CONCEPTS
ELECTROMAGNETIC BOREHOLE TELEMETRY BREAKTHROUGHS

Enhanced Signal Quality:
-
Achieve over 90% decode rate using sNRL technology by effectively removing in-band noise, significantly improving raw telemetry data quality which was only at a 30% decode rate (current state-of-the-art DSP: 63% decode rate).
Cost Savings for the Oil Industry:
-
Eliminate decoding errors, saving approximately $2 million per rig on average.
Market Potential:
-
Total land-based rigs: 1,501 (781 in the US + 720 internationally).
-
Total potential savings: $3 billion annually (1,501 rigs * $2 million).
Potential Licensing Revenue Opportunity:
-
Charge 10% for licensing on average cost savings per rig:
-
Annual licensing revenue potential: $300 million.
-
Monthly licensing revenue potential: $25 million.
-
With only 10% market penetration, this translates to an annual licensing revenue of $30 million or $2.5 million monthly licensing revenue across the global market
-
Strategic Advantage:
-
First-mover advantage in a foundational technology that can transform data reliability in oil-field services.
-
Based on beyond state-or-the-art results, 100% market saturation is inevitable becoming the de facto industry standard.
sNRL's patented FSDSP surpasses the state-of-the-art DSP in the oil-field services industry based on analysis and results of over 100 EM Borehole Telemetry datasets

MARKET POTENTIAL OF ADDITIONAL PROFORMA FIELDS-OF-USE

NOTE: Each of these markets represent only a subsample of the total markets available to sNRL in AUDIO and AI.
| First-Year Revenue Projections | US Hearing Aid | Global Hearing Aid | Global Smartphones | Audio Apps | Total Revenue | Monthly Distribution |
|---|---|---|---|---|---|---|
| Total Number of Devices/Apps | 2,500,000 | 8,405,000 | 7,430,000,000 | 14,860,000,000 | --- | --- |
| 1st Year Market Penetration | 2% | 1% | 0.5% | 0.5% | --- | --- |
| License Cost Per Device/App | $1.00 | $1.00 | $1.00 | $0.10 | --- | --- |
| Cumulative Audio License | $50,000 | $84,050 | $37,150,000 | $7,430,000 | $44,714,050 | --- |
| Monthly Distribution | $4,166.67 | $7004.17 | $3,095,933.33 | $619,166.67 | --- | $3,726,171 |
| First-Year Revenue Projections | Digital Signal Processing | System on a Chip (Edge) | AI as a Service (AIaaS) | Total Revenue | Monthly Distribution |
|---|---|---|---|---|---|
| Market Size | $29,407,300,000 | $167,200,000,000 | $15,090,000,000 | --- | --- |
| Market Share Penetration | 0.1% | 0.0% | 0.1% | --- | --- |
| Cumulative Share of Market | $29,407,300 | $0 | $15,090,000 | $44,497,300 | --- |
| Monthly Distribution | $2,450,608 | $0 | $1,257,500 | --- | $3,708,108 |

AI SIGNAL PROCESSING CLOUD AND CHIP Fractional Calculus Libraries
FIRST-YEAR REVENUE MARKET PROJECTIONS FOR THESE SPECIFIC AI FIELDS-OF-USE

AUDIO Fractional Calculus Libraries
FIRST-YEAR REVENUE MARKET PROJECTIONS FOR THESE SPECIFIC AUDIO FIELDS-OF-USE
# sNRL MARKET POTENTIAL
# sNRL MARKET POTENTIAL
MARKET POTENTIAL OF ADDITIONAL PROFORMA FIELDS-OF-USE

NOTE: Each of these markets represent only a subsample of the total markets available to sNRL in AUDIO and AI.
AI SIGNAL PROCESSING CLOUD AND CHIP Fractional Calculus Libraries
SECOND-YEAR REVENUE MARKET PROJECTIONS FOR THESE SPECIFIC AI FIELDS-OF-USE


AUDIO Fractional Calculus Libraries
SECOND-YEAR REVENUE MARKET PROJECTIONS FOR THESE SPECIFIC AUDIO FIELDS-OF-USE
| Second-Year Revenue Projections | US Hearing Aid | Global Hearing Aid | Global Smartphones | Audio Apps | Total Revenue | Monthly Distribution |
|---|---|---|---|---|---|---|
| Total Number of Devices/Apps | 2,700,000 | 9,077,400 | 7,580,000,000 | 15,160,000,000 | --- | --- |
| 1st Year Market Penetration | 6% | 3% | 1.5% | 1.5% | --- | --- |
| License Cost Per Device/App | $1.00 | $1.00 | $1.00 | $0.10 | --- | --- |
| Cumulative Audio License | $162,000 | $272,322 | $113,700,000 | $22,740,000 | $136,874,322 | --- |
| Monthly Distribution | $13,500 | $22,694 | $9,475,000 | $1,895,000 | --- | $11,406,194 |
| Second-Year Revenue Projections | Digital Signal Processing | System on a Chip (Edge) | AI as a Service (AIaaS) | Total Revenue | Monthly Distribution |
|---|---|---|---|---|---|
| Market Size | $31,730,476,700 | $180,074,400,000 | $19,903,710,000 | --- | --- |
| Market Share Penetration | 0.6% | 0.1% | 0.6% | --- | --- |
| Cumulative Share of Market | $190,382,860 | $180,074,400 | $119,422,260 | $489,879,520 | --- |
| Monthly Distribution | $15,865,238 | $15,006,200 | $9,951,855 | --- | $40,823,293 |
# sNRL PATHS TO MARKET
A $12 M Investment Enables sNRL to Build
ONE MASTER LIBRARY Providing Access to Multiple Markets
One Investment,
Multiple Revenue Streams
A $12 million dollar investment provides sNRL access to multiple markets at an estimated $5M burn rate per year employing 34 people at sNRL.
Potential for Rapid Product Launch
As the Fractional Calculus code libraries, toolboxes, and AI are completed, we can launch multiple products across distinct fields, each with the potential to generate revenue within a year.
Once the core FSDSP SDK, API, FC-AI, and hardware solutions are developed, they can be adapted for various applications with minimal modifications to the front and back end designs for specific data types and formats, while the foundational FSDSP and FC-AI algorithms remain unchanged.
This approach provides a faster path to market for the rollout of products across all fields after the initial development of the fractional calculus SDK, API, and AI libraries.
FRACTIONAL CALCULUS HAS APPLICATIONS IN NEARLY ALL
AREAS OF SCIENCE, MEDICINE, TECHNOLOGY, AND ENGINEERING
# sNRL FIELDS OF USEFIELDS-OF-USE WHERE FRACTIONAL CALCULUS WILL HAVE AN IMPACT
Listed below are some identified disciplines and industries where FC will make a difference:

-
control theory
-
cybernetics
-
information theory
-
medicine
-
neuroscience
-
neuroengineering
-
cognitive science
-
human behavioral sciences
-
environmental sciences
-
meteorology
-
geophysics
-
digital optics
-
broadcasting
-
Finance
-
Marketing
-
control systems
-
robotics
-
mechanical engineering
-
mechatronics
-
sensors/sensing
-
electrical engineering
-
telecommunications
-
Audio
-
Video
-
digital signal processing
-
RADAR
-
SONAR
-
Data Acquisition Systems
-
GPS
-
Quantum Computing
-
Telemedicine (Sensors)
-
Spectroscopy
-
Hyperspectral Imaging
-
Imaging Medical Devices
-
First Responder (XRAY)
-
Heart Rate ID Security
-
RF Communications
-
Bluetooth
-
WiFi
-
Fiber Optics
-
Telescopes (Theoretical Limit)
-
Internet of Things (IoT)
-
Robotics (UAVs, Autopilot)
-
3D Audio
-
Speech Synthesis / Modification
-
Adaptive/Augmented hearing
-
Music Synthesis/Processing
-
Radio
-
Television
-
Medical Data (EEG, MEG, fMRI)
-
Economic Data (stock market algorithms)
-
Environmental Data (temperature)
-
Bionics/Prosthetics

# sNRL COMPETITIVE ADVANTAGE
Competitive Landscape: Unmatched in Fractional Calculus


LIMITED GLOBAL EXPERTISE, BUT WE HAVE THE SOLUTION
As an emerging field of mathematics, only a select few worldwide possess the knowledge and skills to effectively implement fractional calculus into commercially viable products. We have developed pioneering foundational platform technology and were awarded patents that validate our innovation.

FIRST TO MARKET: EXCLUSIVE ADVANTAGE IN FRACTIONAL CALCULUS TECHNOLOGY
Currently, there are no other companies known to be developing fractional calculus libraries for digital signal processing, systems on a chip, or AI toolboxes utilizing fractional calculus.

ILLUMINATING THE BLACK BOX: TRANSPARENT SOLUTIONS THROUGH FRACTIONAL CALCULUS
Our fractional calculus approach in DSP provides clear equations and system models, ensuring transparency in how results are derived and what processes occur within the "black box."
GROUNDBREAKING FRACTIONAL CALCULUS PATENTS WITH PRIORITY BACK TO 2013
We hold exclusive patents for fractional calculus-based algorithms in digital signal processing and fractional order control systems, positioning us as trailblazers in this emerging field.

Competitive Landscape: Unmatched in Fractional Calculus
# sNRL COMPETITIVE ADVANTAGECLOSEST COMPETITORS
A Unique Edge in a Competitive Landscape: The Power of Fractional Calculus in Our Solutions

ARCHETYPE AI (AI Start-Up)
Company: Archetype AI is a Palo Alto-based startup founded by former Google researchers
Approach: Focuses on developing AI to find patterns in and analyze raw data
Limitations: Does not utilize fractional calculus and operates as a "black box," leaving users uncertain about how conclusions are reached.
Stage: Only exists as a research prototype. The company is in talks with potential clients regarding practical implementations, focusing on applications such as predictive maintenance for industrial machinery, energy demand forecasting, and traffic management solutions.
Funds Raised To-Date: $13 Million in Venture Funding
RENESAS ELECTRONICS CORPORATION (Established DSP and Chip/Board Maker)
Company: Renesas is a Japanese semiconductor manufacturer headquartered in Tokyo, Japan
Approach: Renesas' Reality AI Tools allows engineers to generate and build TinyML/Edge AI models based on advanced signal processing. Users can automatically explore sensor data and generate optimized models.
Limitations: Based on background research, Renesas does not utilize fractional calculus in DSP or their AI.
Stage: Established since 2002, Renesas offers a wide range of software, boards, simulation & design tools.
Market Capitalization: As of October 2024 Renesas Electronics has a market cap of $26.03 Billion USD
Competitive Advantage: Identified competitors do not use fractional calculus methodologies and lack foundational insights provided by fractional calculus in data analysis, signal processing, or modeling of control systems.

# FRACTIONAL CALCULUS TECHNOLOGY INVESTMENT

Why Invest in sNRL and our Patented Technology?

sNRL's PATENTED FC ALGORITHMS - FROM MATLAB TO COMMERCIAL VIABILITY
sNRL has developed, tested, and validated fractional calculus toolbox libraries in MATLAB, backed by our patents, placing us ahead of competitors. Your investment will convert and modernize these toolbox libraries from MATLAB to commercially viable solutions as an API, SDK, and embedded chipsets.

FRACTIONAL CALCULUS IS INEVITABLE
It’s not a question of if, but when fractional calculus will become ubiquitous in technology. As we strive to accurately describe complex systems and behaviors, fractional calculus is essential for capturing the realities of our world. By investing now, you position yourself at the forefront of this inevitable transition, becoming part of a revolutionary movement that will shape the future of technology.

ONE MASTER LIBRARY: A PLATFORM FOR MULTIPLE SECTORS
AND THE FUTURE OF FRACTIONAL CALCULUS TECHNOLOGIES
One Master Toolbox Library is the cornerstone of our innovations, encapsulating the foundational mathematics for applying fractional calculus to signals, control systems, and AI. As a platform technology, One Master Library will serve as the basis for hundreds of future fractional calculus applications in multiple sectors in nearly all areas of science, medicine, technology, and engineering. With sNRL at the helm, we hold the key to changing the world through these transformative FC algorithmic libraries that will redefine how we understand and interact with complex systems and the real world.
# FRACTIONAL CALCULUS TECHNOLOGY INVESTMENT
Value-Driven Partnerships for Human Advancement
Unlocking Value: From Research to Revenue with Fractional Calculus

# sNRL INVESTMENT PARTNER

sNRL BUILT AND ESTABLISHED FOUNDATIONS FOR SUCCESS
- We have developed a foundational set of FC toolbox libraries in MATLAB, hold key patents in fractional calculus algorithms, and have more patents ready to file.
- We built and maintain our own infrastructure which includes an internal communications network, a video conferencing platform, and a code repository, enabling us to begin building commercially viable FC solutions immediately upon investment while protecting the security of our technology.

PROVEN MARKET-READY SOLUTIONS ACROSS INDUSTRIES
- With validated and successful proof of concepts in fields such as borehole telemetry, audio, and neuroscience, we know our fractional calculus solutions work.
- With your investment, we can launch our FC libraries from the laboratory into commercially viable enterprise solutions across a vast and diverse industrial, medical, and technological market, unlocking substantial growth potential for our business and significant returns for our investors.
Investing in Tomorrow's Breakthroughs Today:
Path to Market and Vision for Innovation

# sNRL INVESTMENT PARTNER

RAPID TRANSITION TO COMMERCIALIZATION
- Our expedited path to market positions us strategically ahead of competitors.
- Investment will serve as the catalyst to accelerate the development of APIs, SDKs, and comprehensive FC toolbox libraries for seamless integration into AI and other applications.
- With a clear path to market and the groundwork already laid, we are also poised to initiate the development of our SCaLiNG Layered Matrix Network (SLMN) AI.

PARTNERING FOR A TRANSFORMATIVE FUTURE
- By investing in sNRL, you become a key partner in our mission to advance science and expand the boundaries of technology. Together, we will harness fractional calculus to redefine industry standards, introduce entirely new technologies, and reshape the future of AI.
- Together, by leveraging the power of fractional calculus, we can drive a technological revolution that opens new scientific frontiers and creates a lasting impact across multiple markets to meet the demands of tomorrow—today. Your investment will not only contribute to this momentum but also position you alongside us at the forefront of a paradigm shift in the technological landscape through the integration of fractional calculus, capitalizing on our advanced position in the industry.
# FRACTIONAL CALCULUS TECHNOLOGY INVESTMENT
Seize the Opportunity: Invest in the Future with sNRL
# sNRL INVESTMENT PARTNER
Be a Partner to Catalyze Innovation for a New Era

Building the Algorithms that Shape Our World


The TIME is NOW:
Emerging Fields in Frontier Science:
Fractional Calculus is emerging as a significant field of mathematics while Artificial Intelligence is experiencing exponential growth, both of which have profound applications in all related fields of science and engineering. Only recently in the past 15 years have researchers and academics really begun to explore Fractional Calculus as an applied discipline, as advancements in computer processing power and sensor technologies have made possible the handling of the breadth of calculations which had previously precluded any serious application of the subject.
Integration of Fractional Calculus
Into Deep Learning and AI Algorithms:
Advances in Processors have Opened
the Door to Breakthrough Innovation:
Likewise, these same advances in computer processing power have led to an explosion in Artificial Intelligence technologies, with new discoveries occurring on an almost daily basis. Still, while AI is thought of as the next frontier, AI is still in its early stages of development. Furthermore, dedicated research and development of Fractional Calculus currently exists only in a few rarefied universities and laboratories.
In order to push the envelope of Frontier Science, AI must be given access to the power, accuracy, robustness, and efficiency of fractional calculus.
# FRACTIONAL CALCULUS AND ARTIFICIAL INTELLIGENCE INSTITUTE
Fractional Calculus and Artificial Intelligence Institute:
R&D Think Tank and Educational Institute

# FRACTIONAL CALCULUS AND ARTIFICIAL INTELLIGENCE INSTITUTE
Fractional Calculus and Artificial Intelligence Institute:
R&D Think Tank and Educational Institute




Together, with your financial support, mentorship, and partnership, we can serve as the cornerstone for the foundation of the Fractional Calculus and Artificial Intelligence Institute - something the world has never seen before - and lead the way bringing Fractional Calculus and AI to the forefront of this next frontier of science and mathematics, laying the foundation for future technologies to level up humanity. We believe that the establishment of the Fractional Calculus and Artificial Intelligence Institute will become a Bifurcation Event in the history of science and mathematics as humanity embarks on a new trajectory of knowledge and understanding of the world around us.
A crucial step for the future is to consolidate the groundbreaking work we have done to push the development and adoption of the power of Fractional Calculus and integrate this expansive mathematics into deep learning and AI to spawn the next scientific revolution.
We propose to establish a first of its kind Fractional Calculus and Artificial Intelligence Institute which would serve as a think tank and interdisciplinary research laboratory of scientists, mathematicians, computer programmers, doctors, and students. We expect the Fractional Calculus and Artificial Intelligence Institute to become a leader in the development of the foundational mathematics and algorithms of Fractional Calculus and AI in multiple fields of science and engineering including aerospace, automotive, robotics, energy, and medicine to achieve breakthrough technological advancements with beyond state-of-the-art performance.
Personnel of the R&D lab of sNRL form a core group to serve as a basis to establish a "first-of-its-kind" Fractional Calculus and Artificial Intelligence Institute.
# FRACTIONAL CALCULUS AND ARTIFICIAL INTELLIGENCE INSTITUTE

- Develop Fractional Calculus toolbox libraries tailored for machine-learning and deep-learning applications merging Artificial Intelligence with the advanced digital signal processing capabilities of fractional calculus across a variety of fields-of-use within current and future technologies
- To perform educational outreach, host visiting scholars and scientists, and develop seminars, courses, and educational materials such as textbooks to teach fractional calculus since the mathematics of FC is currently not taught in schools or universities unless part of a specialized curriculum and to educate on the science and promise that deep learning and AI hold for the future.
- To perform basic and advanced research for the continued development of the fields of fractional calculus mathematics and artificial intelligence, their applications, and integration of FC into AI/DL and future technologies such as quantum computers and oscillator-based computers (OBCs)
- To serve as a Clearinghouse for establishing the foundational mathematics and algorithms of Fractional Calculus and their implementation into AI algorithms across a variety of fields of use and scientific disciplines
- To work with universities, laboratories, industry, and governmental agencies collaborating on research projects and technological development to propel the fields of FC and AI forward
Core functions of the
Fractional Calculus and Artificial Intelligence Institute include:
Fractional Calculus and Artificial Intelligence Institute:
R&D Think Tank and Educational Institute


The Institute in conjunction with sNRL would also serve to:
-
Research and identify legacy technology upgrades and new-use cases to add to the knowledge-base of fractional calculus applications and explore enhancement by AI
-
Assist sNRL in practical implementation of identified upgrades and FC-AI applications
-
Create a repository of FC and AI algorithms and a platform for easy integration of algorithm libraries developed at the institute for licensing by sNRL through sNRLTECH
-
Guide development of Licensable Software Development Kits (FSDSP SDK), API, and FSDSP Chipsets that use FC-AI to be geared towards specific types of data sets, fields-of-use, or applications and provide a laboratory test bed for these SDK, API, and Chipsets
-
Provide a vehicle for joint development agreements with scientists, companies, industries, or governmental organizations or agencies that wish to utilize our FC-AI technology
sNRL then may also further serve to fund, protect, patent, license, and commercialize technologies developed by the Fractional Calculus and Artificial Intelligence Institute which provide both sNRL and the inventor protection and a pathway to market for one’s work.
The Fractional Calculus and Artificial Intelligence Institute expands the Research and Development capabilities of sNRL

Fractional Calculus and Artificial Intelligence Institute:
R&D Think Tank and Educational Institute
# FRACTIONAL CALCULUS AND ARTIFICIAL INTELLIGENCE INSTITUTE


# sNOISE RESEARCH LABORATORY
Meet the Core Team



The fractional.
“The difference between ordinary and extraordinary is the little extra”.

# sNOISE RESEARCH LABORATORY
Fractional Scaling
Digital Signal Processing
Licensing Information:
The sNoise Research Laboratory has intellectual property rights relating to technology described in this document. In particular, and without limitation, these intellectual property rights include the algorithms and methods of Fractional Scaling Digital Signal Processing, Fractional Scaling Digital Filters, and Fractional Order Control Systems which are covered by one or more patents or pending patent applications. Commercial use of algorithms and methods of Fractional Scaling Digital Signal Processing, Fractional Scaling Digital Filters, and/or Fractional Order Control Systems is strictly prohibited without a licensing agreement obtained through the sNoise Research Laboratory Technology Office (tech@snoiselab.com). Other uses of this document, including reproduction and distribution, selling or licensing copies, or posting to personal, institutional, or third party websites are prohibited.
sNoise®™ is a registered trademark of the sNoise Research Laboratory.
Patented and Patent Pending Technology:
-
U.S. Patent No. 9,740,662 issued August 22, 2017 claiming priority to U.S. Provisional Patent Applications Nos. 61/870,052 and 61/870,064 filed on August 26, 2013 and No. 62/039,684 filed on August 20, 2014.
-
U.S. Patent No. 10,164,609B2 issued December 25, 2018; US version of International Patent Application No. PCT/US15/46184
-
International Patent Application No. PCT/US15/46184 filed on August 20, 2015 claiming priority to U.S. Provisional Patent Application No.62/039,684 filed on August 20, 2014.
-
International Patent Application No. PCT/US17/44257 filed on July 27, 2017 claiming priority to U.S. Provisional Patent Application No. 62/367,464 filed on July 27, 2016.
-
U.S. Patent No. 10,169,293B2 issued January 1, 2019; filed on August 21, 2017, Continuation of U.S. Patent No. 9,740,662.
-
U.S. Patent No. 10,727,813B2 issued July 28, 2020; filed on July 27, 2017.
CONTACT:
For All Licensing Inquires: tech@snoiselab.com
For Scientific Inquiries: Jeffrey.Smigelski@snoiselab.com
v22.24FEB2025
sNoise Research Laboratory
13719 23 Mile Road #116, Shelby Township, MI 48315
sNRL@snoiselab.com
Dr. Jeffrey R. Smigelski, Ph.D.
Jeffrey.Smigelski@snoiselab.com

Copyright © 2025, sNoise Research Laboratory, USA. All rights reserved.
Agenda
# AGENDA PROTOCOL